Задачи с лестницей с решением

Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен:

Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?

Задача сводится к нахождению гипотенузы прямоугольного треугольника, по теореме Пифагора она равна:

Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?

Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?

Это задание ещё не решено, приводим решение прототипа.

Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен:

Источник

Разбор олимпиадной задачи — Лесенка

Задача взята с acmp.ru (Время: 1 сек. Память: 16 Мб Сложность: 55%)

Очень хорошая задача на понимание рекурсии, рекомендую.

Лесенкой называется набор кубиков, в котором каждый более верхний слой содержит кубиков меньше, чем предыдущий. Требуется написать программу, вычисляющую число лесенок, которое можно построить из N кубиков.

Входные данные:
Во входном файле INPUT.TXT записано натуральное число N (1 ≤ N ≤ 100) – количество кубиков в лесенке.

Выходные данные:
В выходной файл OUTPUT.TXT необходимо вывести число лесенок, которые можно построить из N кубиков.

Для начала, предлагаю попробовать вручную построить лесенки. В частности для второго примера:

Программа должна генерировать лесенки по определенному алгоритму, чтобы его лучше понять, предлагаю посмотреть на следующую картинку, где показано как из одной лесенки программа может получить другую:

Есть у нас лесенка из 7 кубиков, сложенных в ряд. В следующий ряд мы можем положить 1, 2 и 3 кубика. 4 кубика переложить уже нельзя, т.к. тогда в первом будет меньше чем во втором. Дальше аналогичным образом обрабатывается второй ряд, третий, четвертый и т.д. Т.е. налицо рекурсивный алгоритм.

Первый вариант решения (не пройдет все тесты) мог бы выглядеть так:

В функции main выполняется генерация кубиков в первом уровне. В нем может быть от 1 до n кубиков. Этот код вынесен в main потому что остальные уровни генерируются чуть-чуть иначе, в них должно учитываться число кубиков на предыдущем уровне (для первого уровня нет предыдущего).

Функция get_count возвращает единицу (лесенку удалось сгенерировать) если количество кубиков равно нулю — т.е. мы каким то корректным образом строили лесенку и у нас кончились кубики. Для остальных случаев мы запускаем рекурсивную функцию с различными наборами данных, уменьшая количество кубиков на текущем уровне и увеличивая на следующем.

Этот код будет работать корректно, но долго (не пройдет тесты по времени). Чтобы найти проблемное место можно заставить функцию get_count перед своим завершением выводить входные данные и результат (count) в файл или на экран. Мы увидим, что она много раз вызывается для отрицательных значений количества кубиков на уровне (n). Необходимо добавить проверку, что n — level больше ноля.

В последнем варианте программы убран также цикл из функции main. В самом деле, можно обобщить генерацию первого и последующих уровней если предположить что перед первым есть «нулевой», на котором находится n+1 кубик (заведомо шире любой лесенки из n кубиков).

Источник

Задачи с лестницей с решением

От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.

Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке. Таким образом, задача сводится к нахождению гипотенузы прямоугольного треугольника; обозначим её за По теореме Пифагора:

От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.

Пусть длина искомой стороны равна Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке, тогда — катет получившегося прямоугольного треугольника. По теореме Пифагора:

Следовательно, длина искомой стороны равна 9.

Источник

Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену

Условие задачи:

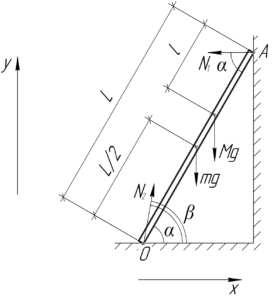
Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену, а нижним – в пол под углом 60° к горизонту. На лестнице на расстоянии 1 м от её верхнего конца стоит человек массой 60 кг. Под каким углом к горизонту направлена сила, с которой пол действует на нижний конец лестницы?

Задача №3.1.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

\(m=15\) кг, \(L=3\) м, \(\alpha=60^\circ\), \(l=1\) м, \(M=60\) кг, \(\beta – ?\)

Решение задачи:

На лестницу действуют следующие силы: сила тяжести лестницы \(mg\), сила тяжести человека \(Mg\), сила нормальной реакции \(N_1\) в точке A и сила реакции \(N_2\) в точке O. Так как лестница находится в равновесии, то запишем первое условие равновесия (первый закон Ньютона) в проекции на обе оси и второе условие равновесия (правило моментов) относительно точки O.

\[\left\< \begin
\cdot \sin \beta = mg + Mg \;\;\;\;(1)\hfill \\
\cdot \cos \beta = \;\;\;\;(2)\hfill \\
mg \cdot \frac <2>\cdot \cos \alpha + Mg \cdot \left( \right) \cdot \cos \alpha – \cdot L \cdot \sin \alpha = 0 \;\;\;\;(3)\hfill \\
\end \right.\]

Поделим равенства (1) и (2) друг на друга:

Из равенства (3) выразим реакцию \(N_1\):

Полученное подставим в (4), тогда:

Окончательная формула примет вид:

Посчитаем численное значение искомого угла \(\beta\):

\[\beta = arctg\left( <\frac<<\left( <15 + 60>\right) \cdot 2 \cdot 3 \cdot tg60^\circ >> <<15 \cdot 3 + 2 \cdot 60 \cdot \left( <3 – 1>\right)>>> \right) = 70^\circ = 1,22\;рад\]

Ответ: 1,22 рад.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Источник

Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до N-й ступеньки?

Начало здесь простое. Вы стоите на лестничном марше и хотите подняться на первую ступеньку — № 1. Для этого надо сделать всего одно действие — подняться на одну ступеньку вверх. Теперь давайте рассмотрим вторую ступеньку, то есть N = 2. Чтобы подняться на неё, имеются два варианта. Вы можете сделать два шага — по одной ступеньке за раз или сразу подняться на вторую ступеньку.

Это практически вся информация, которая нужна вам для решения этой задачи. Чтобы понять, почему, представьте, что вашей целью является ступенька № 3. Впервые в этой ситуации вы не можете попасть на неё одним движением. здесь потребуется комбинация шагов. Существует только два способа попадания на ступеньку № 3: либо в виде короткого одиночного шага (со ступеньки № 2), либо двойного шага (со ступеньки № 1). Мы уже знаем, что для подъема на ступеньку № 1 имеется лишь один вариант. Мы также знаем, что есть всего два способа подняться на ступеньку № 2. Сложите эти варианты (1 + 2 = 3), и вы получите число способов, позволяющих подняться на ступеньку № 3.

Та же самая логика применяется для подъема на каждую следующую ступеньку. Существует два способа, чтобы подняться на ступеньку № 4 — со ступеньки № 2 или со ступеньки № 3. Добавьте число способов подъема на ступеньку № 2 (2) к числу способов, позволяющих оказаться на ступеньке № 3 (3). Это даёт 5 вариантов — число способов, позволяющих оказаться на ступеньке № 4.

Легко продолжить эту серию и дальше. С увеличением числа ступенек число способов подниматься по ним нарастает, как снежный ком, что можно представить в следующем виде:

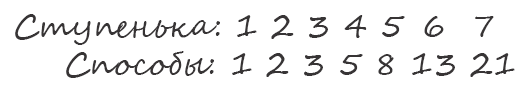
Любому человеку с математической подготовкой нижняя серия покажется до боли знакомой. Так оно и есть. Это последовательность Фибоначчи. (Чуть подробнее о ней ниже.) Интервьюер хочет получить ответ для общего случая из N ступенек.

Это просто число Фибоначчи под номером N. Леонардо Фибоначчи, также известный как Леонардо Пизанский, был самым влиятельным итальянским математиком в Средние века. Именно Фибоначчи понял невероятное превосходство арабскo-индийской позиционной системы исчисления по сравнению с римским обозначением цифр, которое все ещё использовалось в средневековой Европе. При помощи арабско-индийской системы умножение и деление можно было свести к алгоритму (еще одно арабское слово). При применении римских чисел эти операции на практике выполнять было сложно. Торговцам приходилось приглашать экспертов и дорого им платить за вычисления, которые те осуществляли при помощи абаков. В 1202 году Фибоначчи написал Liber abaci — руководство по использованию абака, в котором он расхваливал арабские числа своим читателям, которые были, скорее всего, настроены к ним скептически. В этой книге также описывается и та серия чисел, которую мы теперь называем по его фамилии. Однако её изобрел не Фибоначчи. Эта последовательность была известна еще индийским ученым, жившим в VI веке.

Напишите 1, а затем добавьте еще 1 рядом. Сложите их и получите сумму (2), которая затем добавляется к формируемой последовательности:

Для получения каждого нового члена лишь складывайте последние два числа в ряду/ Серия примет следующий вид.

1 1 2 3 5 8 13 21 34 55 89 144…

Поклонники теории заговоров отыскивают серии Фибоначчи в самых неожиданных местах. Хотите перевести расстояние из миль в километры? Воспользуйтесь соседними числами Фибоначчи (55 миль в час = 89 километров в час). В следующий раз, когда у вас окажется свободное время, посчитайте небольшие дольки, из которых состоит кожура ананаса, и вы обнаружите, что они образуют два накладывающихся друг на друга набора спиралей, идущих в противоположных направлениях. В одной из них восемь долей, в другой тринадцать. Оба этих числа относятся к серии Фибоначчи. Аналогичные закономерности можно увидеть в сосновых шишках, подсолнухах и артишоках. Случайность? Вряд ли, если учесть тот факт, что последовательность Фибoначчи проявила себя и в Коде Да Винчи (в виде комбинации для вскрытия сейфа), и в этом вопросе на собеседовании, который задают в компании, стремящейся к информационному доминированию во всем мире (Google, если вы не поняли).

Источник