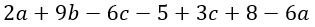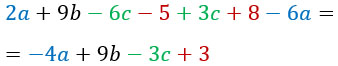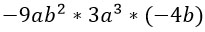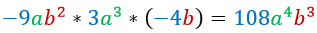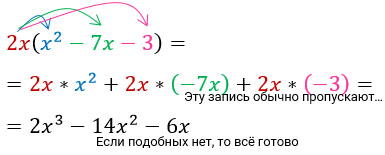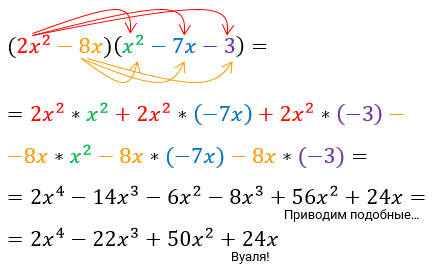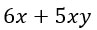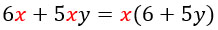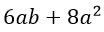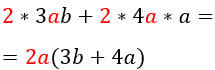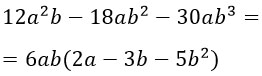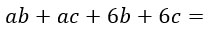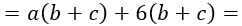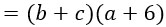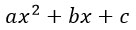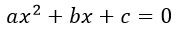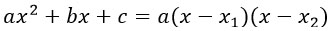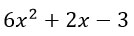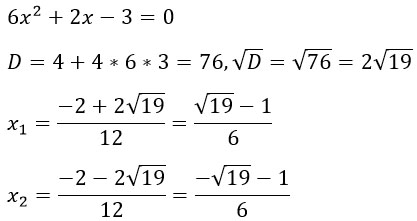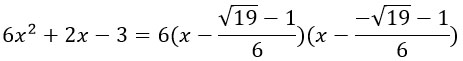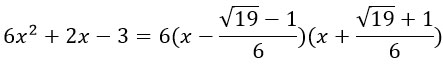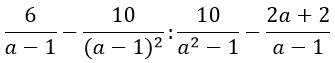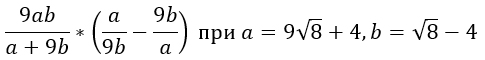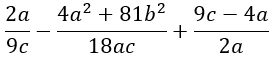Упростить выражение чтобы он выбрал правильную лестницу

Упростить выражение

Что значит упростить выражение

Когда говорят упростить выражение, подразумевают конкретные математические действия с этим выражением, в результате чего оно примет иной вид.

Такими действиями могут быть раскрытие скобок, внесение и вынесение множителя за скобку, деление (сокращение), умножение, возведение в степень, приведение дробей к общему знаменателю и много других операций.

При этом часто используют формулы сокращенного умножения и теоремы, а в тригонометрии от простых формул приведения до самых сложных тригонометрических выражений.

Чем старше школьник, тем больше формул он знает и обладает богатым арсеналом математических действий.

В чем смысл таких действий

Задачи на упрощение выражений встречаются с самых младших классов. Дети сами того не осознавая, учатся шевелить мозгами в нужном направлении, чтобы преобразовать одно выражение в другое.

Разумеется, все задания составляются таким образом, что в любом случае они приводятся к более простому виду или подходящему для дальнейших операций.

Однако, при таком подходе теряется общий смысл поставленной задачи.

Когда ученик слышит, что надо что-то упростить, то машинально начинает перебирать всевозможные математические действия в голове, не задаваясь вопросом, а для чего упрощать?

Приведем наглядный пример

Допустим, сказано упростить выражение (a+b) 2 . В этом случае абсолютно каждый нормальный школьник раскроет скобки и будет доволен самим собой. Без сарказма это действительно так и это нормально.

Но вот другая постановка задачи: упростите выражение (a+b) 2 , затем подставьте следующие числовые значения a=⅔, b=⅓ и запишите получившееся число.

Кто теперь скажет, что раскрыть скобки, затем подставить a=⅔ и b=⅓, а затем вычислить ответ, это легче, чем сразу найти a+b=⅔+⅓=1? После этого возводи единицу хоть в сотую степень!

Итак, главная цель задач на упрощение выражений в том, чтобы научить вас применять те или иные математические действия над выражениями.

Это обязательно нужно уметь делать. Но более важная проблема в том, чтобы научиться применять необходимые действия в нужный момент и воспользоваться результатом преобразования.

Благо есть онлайн калькуляторы упрощения выражений, например, такой как наш, с помощью которого можно проверить свои вычислительные результаты.

Источник

Упрощение выражений

Результат

Примеры упрощаемых выражений

• Приведение слагаемых
• Упрощение произведений
• Сложные дроби со степенями
• Разложение дроби на простейшие
• Раскрытие скобок в выражении
• Разложение на множители

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Источник

Упрощение выражений

Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.

Приведение подобных слагаемых.

Это самый простой из приемов. Подобными называются те слагаемые, у которых одинаковая буквенная часть. Например, подобными будут выражения 5а и -6а; -3ху и 3ух; 2 и 10. Так вот. Складывать можно только подобные слагаемые; если буквенная часть у слагаемых различна, то такие слагаемые складывать уже нельзя. Согласись, если в жизни мы будем складывать яблоки с гвоздями, то у нас какая-то дичь получится) В математике точно так же.

Для примера упростим такое выражение:

Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.

Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.

Умножение одночленов и многочленов.

Не буду спорить — числа ты умножать умеешь. А если к ним добавятся буквы, степени, скобки?

Одночлен — это выражение, состоящее из произведения чисел, букв, степеней, причем необязательно должно быть всё сразу. Удивительно, но просто число 5 тоже является одночленом, так же как и одинокая переменная х.

При умножении одночленов используют правила умножения степеней.

Перемножим три одночлена:

Разными цветами выделю то, что буду последовательно перемножать.

Многочлен — это сумма одночленов.

Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.

Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.

Вынесение общего множителя за скобки.

Разбираться будем на примере.

Дано такое выражение:

Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.

Возьмем другой пример.

Оба числа в слагаемых делятся на 2, значит число 2 — общий множитель. Но еще в этих одночленах есть одинаковая буква а — одна в первой степени, другая — во второй. Берем ее в меньшей степени, т.е. в первой, — это и будет второй общий множитель. В общем, получится вот такая запись:

Ну и давайте третий пример, только уже без комментариев.

Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).

Разложение многочлена на множители способом группировки.

Если надо разложить многочлен на множители, то способ группировки тебе пригодится.

Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки.

На примере будет яснее)

Беру пример самый простой, чисто для понимания того, что надо делать.

В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.

Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:

Разложение квадратного трехчлена на множители.

Пусть дан квадратный трехчлен:

Чтобы разложить его на множители надо решить квадратное уравнение

Далее корни уравнения х₁ и х₂ подставить в следующую формулу:

Возьмем вот такой трехчлен:

Найдем корни квадратного уравнения.

Подставим их в формулу для разложения квадратного трехчлена на множители:

Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:

Еще могут тебе пригодится:

— умение сокращать дроби;

А вот такие задания могут тебе встретится на экзамене.

2) Найти значение выражения при заданных значениях переменных:

3) Найти значение выражения при заданных значениях переменных:

Подобных заданий много — их все не уместишь)

Источник

Решение задач по математике онлайн

С помощью данной математической программы вы можете упростить многочлен.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (приводит подобные)
— раскрывает скобки
— возводит многочлен в степень

Программа упрощения многочленов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать свои знания по математике и/или алгебре.

Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Произведение одночлена и многочлена. Понятие многочлена

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
\( 5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\( xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)

Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.

Например, многочлен
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.

Представим все слагаемые в виде одночленов стандартного вида:
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 = \)
\( = 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 \)

Приведем в полученном многочлене подобные члены:
\( 8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных. Такие многочлены называют многочленами стандартного вида.

За степень многочлена стандартного вида принимают наибольшую из степеней его членов. Так, двучлен \( 12a^2b — 7b \) имеет третью степень, а трехчлен \( 2b^2 -7b + 6 \) — вторую.

Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени. Например:
\( 5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 \)

Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.

Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:

Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.

Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.

Преобразование (упрощение) произведения одночлена и многочлена

С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
\( 9a^2b(7a^2 — 5ab — 4b^2) = \)
\( = 9a^2b \cdot 7a^2 + 9a^2b \cdot (-5ab) + 9a^2b \cdot (-4b^2) = \)
\( = 63a^4b — 45a^3b^2 — 36a^2b^3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \( (a + b)^2, \; (a — b)^2 \) и \( a^2 — b^2 \), т. е. квадрат суммы, квадрат разности и разность квадратов. Вы заметили, что названия указанных выражений как бы не закончены, так, например, \( (a + b)^2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и b. Однако квадрат суммы а и b встречается не так уж часто, как правило, вместо букв а и b в нем оказываются различные, иногда довольно сложные выражения.

Выражения \( (a + b)^2, \; (a — b)^2 \) нетрудно преобразовать (упростить) в многочлены стандартного вида, собственно, вы уже встречались с таким заданием при умножении многочленов:
\( (a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2 = \)
\( = a^2 + 2ab + b^2 \)

Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.

\( (a + b)^2 = a^2 + b^2 + 2ab \) — квадрат суммы равен сумме квадратов и удвоенного произведения.

\( (a — b)^2 = a^2 + b^2 — 2ab \) — квадрат разности равен сумме квадратов без удвоенного произведения.

\( a^2 — b^2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Источник