У лестницы n ступенек пронумерованных числами 1 2 n снизу вверх

Задача про лестницу

Решаю задачу про лестницу:
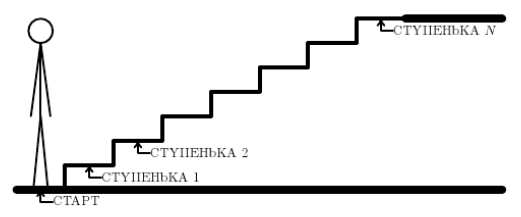
У лестницы n ступенек, пронумерованных числами 1, 2, . n снизу вверх. На каждой ступеньке написано число. Начиная с подножия лестницы (его можно считать ступенькой с номером 0), требуется взобраться на самый верх (ступеньку с номером n). За один шаг можно подниматься на одну или на две ступеньки. После подъёма числа, записанные на посещённых ступеньках, складываются. Нужно подняться по лестнице так, чтобы сумма этих чисел была как можно больше.

Решение выходит за границы массива.
Помогите понять, где ошибка

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Задача про Лестницу
Условия формулируются так: Есть лестница высотой в n ступенек (плюс «нулевая» — площадка, где мы.

Задача про взлом кода из книги Эрика Фримена про основы javascript в конце 5 главы.
читаю книгу Эрика Фримена про основы javascript.В конце 5 главы есть задачка про взлом кода.Никак.

Задача на перебор вариантов. Задача Л.Эйлера. Про чиновника
Задача Л.Эйлера. Некий чиновник купил лошадей и быков на сумму 1770 талеров. За каждую лошадь он.

Нарисовать лестницу
Разработать программу для рисования лестницы. Пользователь вводит количество ступенек. Использовать.

Добавлено через 1 минуту
То есть ты выбегаешь за размеры списка. Ибо n = 3, то есть элементы списка под индексами 0,1,2. А ты бежишь по циклу до n + 1 = 4, то есть заходишь еще и в индекс 3, которого нет.

Добавлено через 2 минуты

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Комбинаторика подъёма на лестницу
Всем привет! Имеется лестница из 10 ступенек, подниматься можно наступая на каждую ступеньку или.

Массив описывает лестницу
Дан упорядоченный массив целых чисел. Он описывает лестницу, разность соседних элементов — высота.

Комбинаторика подъёма на лестницу
Всем привет! Имеется лестница из 10 ступенек, подниматься можно наступая на каждую ступеньку или.

Нарисовать лестницу из восьми перекладин
Создать программу, которая реализует графическими средствами языка программирования Pascal такое.

Вывести лестницу из отрезков определённой длины
14. Вывести лестницу из отрезков определённой длины. Длина (например, 14) и количество ступенек.

Написать процедуру, которая рисовала бы лестницу
Написать процедуру, которая рисовала бы лестницу. Данные: число ступенек, длина самой маленькой.

Источник

Лекция 4. Динамическое программирование.

1 Лекция 4. Динамическое программирование.

2 План лекции Суть динамического программирования Преимущества перед «наивными» методами решения Динамика и рекурсия. Числа Фибоначчи Задача о кузнечике Стоимость маршрута в матрице Наибольшая общая подпоследовательность 2

3 Динамическое программирование Динамическое программирование, динамика это способ решения больших и сложных задач с помощью разделения их на мелкие подзадачи. Главный принцип динамики заключается в запоминании ранее вычисленных значений. 3

4 Задача о лестнице У лестницы n ступенек, пронумерованных числами 1, 2. n снизу вверх. На каждой ступеньке написано число. Начиная с подножия лестницы (его можно считать ступенькой с номером 0), требуется взобраться на самый верх (ступеньку с номером n). За один шаг можно подниматься на одну или на две ступеньки. После подъёма числа, записанные на посещённых ступеньках, складываются. Нужно подняться по лестнице так, чтобы сумма этих чисел была как можно больше. 4

5 Задача о лестнице 5

6 Задача о лестнице 6

7 Задача о лестнице 7

8 Задача о лестнице MAX + 8

9 Задача о лестнице MAX + 9

10 Задача о лестнице MAX + 10

11 Задача о лестнице MAX + 11

12 Задача о лестнице MAX + 12

13 Задача о лестнице MAX + 13

14 Задача о лестнице MAX + 14

15 Задача о лестнице #include using namespace std; int main() < long long n, a[102], b; cin >> n >> a[1]; a[0] = 0; //Если количество ступеней 1, ответ if(n > b; a[i] = max( a[i-1], a[i-2] ) + b; > > cout 16 Динамическое программирование Как правило, динамика выполняется за линейное время O(n). Если посчитать, та же задача про лестницу обыкновенным полным перебором решалась бы за O(2 n-3 ). ДИНАМИКА ВЫГОДНЕЕ ПЕРЕБОРА. 16

17 Динамика и рекурсия Стоит задача вычислить k-е число Фибоначчи элемент последовательности, в которой каждый элемент равен сумме двух предыдущих. a 1 = 1; a 2 = 1; a n = a n-1 + a n

18 Динамика и рекурсия Можно для этого использовать рекурсивную функцию: int fib(int index) < if(index == 1 index == 2) return 1; return fib(index-1) + fib(index-2) >Но что будет делать этот код при больших числах? 18

19 Динамика и рекурсия fib(6) fib(5) fib(4) fib(4) fib(3) fib(3) fib(2) fib(3) fib(2) fib(2) fib(1) fib(2) fib(1) fib(2) fib(1) 19

20 Динамика и рекурсия Динамикой (то есть простым запоминанием результатов) можно избежать повторений в вычислениях: vector a(k, -1); int fib(int index) < if(a[index] 21 Динамика и рекурсия fib(6) fib(5) fib(4) fib(4) fib(3) fib(3) fib(2) fib(2) fib(1) 21

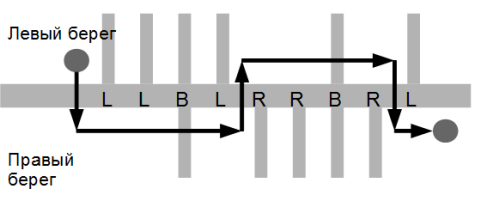
22 Задача о кузнечике/зайчике/ Зайчик прыгает по прямой просеке, для удобства разделённой на n клеток. Клетки пронумерованы по порядку натуральными числами от 1 до n. Некоторые клетки заболочены ( w ): если зайчик прыгнет на такую клетку, ему несдобровать. Некоторые другие клетки просеки поросли вкусной зелёной травой ( ): прыгнув на такую клетку, зайчик сможет отдохнуть и подкрепиться. Зайчик начинает свой путь из клетки с номером 1 и хочет попасть в клетку с номером n, по пути ни разу не провалившись в болото и скушав как можно больше вкусной зелёной травы. Конструктивные особенности зайчика таковы, что из клетки с номером k он может прыгнуть лишь в клетки с номерами k + 1, k + 3 и k + 5. Выясните, какое максимальное количество клеток с травой сможет посетить зайчик на своём пути. 22

23 Задача о кузнечике/зайчике/ 23

24 Задача о кузнечике/зайчике/ Массив динамики изначально занят -1, кроме первого элемента, который равен значит, что на эту клетку заяц попасть не смог. Числа 0 это максимальное количество клеток с травой, которые на своём пути посетил заяц. Логично, что в клетку k заяц может попасть только из клеток k-1, k-3 и k-5. Тогда максимальное количество клеток с травой, посещённых до клетки k включительно, будет равняться максимальному количеству очков среди тех клеток, откуда мы могли прийти, и +1 в том случае, если k сама клетка с травой. 24

25 Задача о кузнечике/зайчике/ 25

26 Задача о кузнечике/зайчике/ 26

27 Задача о кузнечике/зайчике/ +1 MAX 27

28 Задача о кузнечике/зайчике/ +1 MAX 28

29 Задача о кузнечике/зайчике/ MAX 29

30 Задача о кузнечике/зайчике/ vector a(n+2, -1); char c; cin >> c; a[1] = 0; for(int i = 2, i > c; if(c == w ) continue; if(i 31 Стоимость маршрута в матрице Справка: Матрица, или двухмерный массив это массив массивов, т.е. массив, каждый элемент которого тоже массив. int a[10][10]; for(int i=0;i 32 Стоимость маршрута в матрице Имеется матрица размера NxM, в каждой клетке которой записано некоторое положительное число. Какую максимальную сумму можно набрать, двигаясь по матрице из левого верхнего в правый нижний угол при условии, что ходить можно только вниз и вправо? N и M

33 Стоимость маршрута в матрице Пусть a[][] это матрица с числами, а dp[][] это матрица динамики. for(int i = 0; i 34 Стоимость маршрута в матрице a[][] 34

35 Стоимость маршрута в матрице dp[][] 35

36 Стоимость маршрута в матрице dp[][] Восстановление пути: двигаемся с конца, всегда переходя из dp[i][j] в максимальное из dp[i-1][j] и dp[i][j-1] 36

37 Наибольшая общая подпоследовательность Имеются две последовательности символов (или чисел, неважно) длин N и M. Требуется найти их наибольшую общую подпоследовательность (LCS). Пример: a = abcdf b = abdca LCS(a,b) = abc или abd 37

38 Наибольшая общая подпоследовательность В dp[i][j] записана длина наибольшей общей подпоследовательности подстрок искомых строк длин i и j соответственно. Например, dp[2][3] это ответ на задачу для строк ab и abd. for(i = 1..N) for(j = 1..M) if(a[i] == b[j]) dp[i][j] = dp[i-1][j-1] + 1; else dp[i][j] = max( dp[i-1][j], dp[i][j-1] ); 38

39 Наибольшая общая подпоследовательность Чтобы найти саму LCS, надо пройтись по матрице dp[][] и найти места, где dp[i][j] > dp[i-1][j] и dp[i][j] > dp[i][j-1], и после нахождения каждого такого уголка исследовать dp[][] по индексам, строго меньшим, чем у найденного уголка. Это поможет в ситуациях, когда есть больше, чем одна LCS. 39

Источник

У лестницы n ступенек пронумерованных числами 1 2 n снизу вверх

Динамическое программирование

Задача1 Вычислить N -ое число в последовательности Фибоначчи, — 1, 1, 2, 3, 5, 8, … — в которой первые два члена равны единице, а все остальные представляют собой сумму двух предыдущих.

Входные данные: Одно число 1≤N≤70. .

Выходные данные: Одно число — N -ый член последовательности.

Решение: Выпишем условие задачи в виде формул: F1=1, F2=2, Fi=Fi−1+Fi−2,i≥3.

const MaxN = 70;
var i,N : Integer;
F : Array [1..MaxN] of Integer;
begin

Задача 2 Мячик на лесенке

На вершине лесенки, содержащей ступенек, находится мячик, который начинает прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну или через 2. (То есть, если мячик лежит на 8-ой ступеньке, то он может переместиться на 5-ую, 6-ую или 7-ую.). Определить число всевозможных «маршрутов» мячика с вершины на землю.
Входные данные:
Одно число 1≤N≤40. .
Выходные данные:
Одно число — количество маршрутов.

Входной файл	Выходной файл
4	7
39	12960201916
13	1705

Есть только один способ попасть на первую ступеньку.
— попасть на 2-ую можно 2-мя способами: прыгнув на неё сразу или прыгнув с 1-ой ступеньки.
— попасть на 3-ую можно 4-мя способами:
1) прыгнув на неё сразу
2) прыгнув на 1-ую, потом на 3-ю
3) прыгнув на 2-ую, потом на 3-ю
3) прыгнув на 1-ую ступеньку, потом на 2-ую, потом на 3-ю.

На ступеньки начиная с 4-ой можно попасть с 3-х предыдущих. Мы знаем, сколькими способами можно попасть на каждую ступеньку из предыдущих. Общий принцип: Количество вариантов как попасть в какое-то состояние равно сумме количеств вариантов как попасть в предыдущие состояния.

var f1,f2:text;
a: array [0..70] of integer;
i,n: byte;
begin
assign(f1, ‘input.txt’); reset(f1);
assign(f2, ‘output.txt’); rewrite(f2);
read(f1,n);
a[1]:=1;
a[2]:=2;
a[3]:=4;
for i:=4 to n do
a[i]:=a[i-3]+a[i-2]+a[i-1];
writeln(f2,a[n]);
close(f1);
close(f2);
end.

Задача 3 329. Лесенка-2 (Время: 1 сек. Память: 16 Мб )

Вова стоит перед лесенкой из N ступеней. На каждой из ступеней написаны произвольные целые числа. Первым шагом Вова может перейти на первую ступень или, перепрыгнув через первую, сразу оказаться на второй. Также он поступает и дальше, пока не достигнет N-ой ступе- ни. Посчитаем сумму всех чисел, написанных на ступенях через которые прошел Вова. Требуется написать программу, которая определит оптимальный маршрут Вовы, при котором, шагая, он получит наибольшую сумму. Входные данные Входной файл INPUT.TXT содержит в первой строке натуральное число N – количест- во ступеней лестницы. Во второй строке через пробел заданы числа, написанные на ступенях лестницы, начиная с первой. Количество ступеней не превышает 1000, числа, написанные на ступенях, не превосходят по модулю 1000. Выходные данные Выходной файл OUTPUT.TXT должен содержать в первой строке наибольшее значение суммы. Во второй строке должны быть записаны через пробел номера ступеней по возрастанию, по которым должен шагать Вова.

Разбор Для решения задачи используем идею динамического программирования. Обозначим че- рез S(i) – наибольшую сумму в оптимальном маршруте Вовы от первой ступеньки до i-й. Имеем S(1)=a(1), S(2)=a(1)+a(2). На i-ю ступеньку он может попасть или с i-1-й или с i-2-й, из этих двух случаев выбираем тот, для которого имеем наибольшее значение, т.е. S(i)=max+a(i). Последовательно рассчитаем значения S для i=1, 2, . N. Для определения оптимального маршрута просмотрим полученные значения S(i) в обратном порядке.

Источник

У лестницы n ступенек пронумерованных числами 1 2 n снизу вверх

Динамическое программирование (или коротко динамика) — это подход к решению достаточно широкого класса задач, в котором решение исходной задачи строится на основе решения подзадач. Слово «программирование» в названии «динамическое программирование» имело не тот смысл, что сейчас: когда Ричард Беллман придумал этот термин, составление программ не было массовой профессией и названия для этой профессии не было. В те времена программирование означало «планирование» и под «динамическим программированием» понималось оптимальное планирование многоступенчатых процессов.

Совсем в общем виде подход состоит в том, чтобы вместо одной исходной задачи, придумать множество подзадач так, чтобы исходная была среди них, но при этом каждая из подзадач «легко» выводится из «предыдущих». Если говорить формально, то сначала определяется множество подзадач. Их мы располагаем в вершинах графа. Дальше мы проводим ориентированные рёбра из одной подзадачи в другую, если решение первой помогает во второй. Если в результате получился «не слишком большой» ациклический граф (если есть циклы, то всё пропало!), то задача решается динамическим программированием. Известно, что вершины ациклического графа можно так обойти, чтобы на каждом шаге не встречать не решённых зависимостей.

Начнём с простого примера: числа Фибоначчи. Они определяются так: $F_1 = 1$, $F_2 = 1$, $F_ = F_ + F_$. Если наша исходная задача — это вычислить $F_n$, то подзадачи — это вычисление $F_1, F_2, \ldots, F_, F_n$. Каждая подзадача $F_i$ легко решается на основе ответов в подзадачах $F_$ и $F_$. Ациклический граф подзадач выглядит следующим образом:

Стандартные види динамики

Включение исходной задачи в семейство зависимых подзадач требует изобретательности, но есть несколько стандартных вариантов. Вот они:

• Вычисляем простую последовательность. Исходную задачу можно включить в вычисление элементов последовательности $x_1, x_2, \ldots, x_n$, подзадачи — вычисление значений $x_i$ для $i \le n$, причём $x_i$ вычисляется на основе фиксированного количества предыдущих членов (как в примере с числами Фибоначчи). Сложность решения — $O(n)$. Пример задачи — числа Фибоначчи и последовательности, заданные рекуррентными соотношениями.
  
• Вычисляем сложную последовательность. То же самое, что в предыдущем пункте, но $x_i$ вычисляется на основе всех предыдущих членов. Сложность решения — $O(n^2)$. Достаточно часто существует оптимизация решения до $O(n \log n)$;
  
• Вычисляем две последовательности. Исходную задачу можно включить в вычисление элементов последовательностей $x_1, x_2, \ldots, x_m$ и $y_1, y_2, \ldots, y_n$. Подзадачи — вычисление конкретных $x_i$ и $y_j$. Каждый из $x_i$ и $y_j$ легко вычисляются на основе фиксированного набора предыдущих членов. Сложность решения — $O(mn)$;
  
• Вычисляем двумерный массив. Исходную задачу можно включить в вычисление элементов прямоугольного массива $x_<11>, x_<12>, \ldots, x_<1m>, x_<21>, \ldots, x_$, подзадачи — вычисление конкретных $x_$, причём $x_$ вычисляется на основе фиксированного количества предыдущих членов. Сложность решения — $O(mn)$. Пример задачи — вычисление редакционного расстояния между двумя строками;
  
• Обрабатываем последовательность. Задача ставится для данной последовательности $x_1, x_2, \ldots, x_n$, подзадачи — та же задача для префиксов $x_1, x_2, \ldots, x_i$, $i

Вводные задачи

A: Мячик на лесенке

На вершине лесенки, содержащей $N$ ступенек, находится мячик, который начинает прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну или через $2$. (То есть, если мячик лежит на $8$-ой ступеньке, то он может переместиться на $5$-ую, $6$-ую или $7$-ую.) Определить число всевозможных «маршрутов» мячика с вершины на землю.

Вводится одно число $0

B: Последовательность из 0 и 1

Требуется подсчитать количество последовательностей длины $N$, состоящих из $0$ и $1$, в которых никакие две единицы не стоят рядом.

На вход программы поступает целое число $N$ $(1 \leqslant N \leqslant 10^5)$.

Выведите количество искомых последовательностей по модулю $10^9+7$.

C: Без трёх единиц

Определите количество последовательностей из нулей и единиц длины $N$ (длина — это общее количество нулей и единиц), в которых никакие три единицы не стоят рядом.

Вводится натуральное число $N$, не превосходящее $40$.

Выведите количество искомых последовательностей. Гарантируется, что ответ не превосходит $2^<31>-1$.

D: Платная лестница

Мальчик подошел к платной лестнице. Чтобы наступить на любую ступеньку, нужно заплатить указанную на ней сумму. Мальчик умеет перешагивать на следующую ступеньку, либо перепрыгивать через ступеньку. Требуется узнать, какая наименьшая сумма понадобится мальчику, чтобы добраться до верхней ступеньки.

В первой строке входного файла вводится одно натуральное число $N \leqslant 100$ — количество ступенек. В следующей строке вводятся $N$ натуральных чисел, не превосходящих $100$ — стоимость каждой ступеньки (снизу вверх).

Выведите одно число — наименьшую возможную стоимость прохода по лесенке.

Одномерное динамическое программирование

E: Радиоактивные материалы

При переработке радиоактивных материалов образуются отходы трех видов — особо опасные (тип A ), неопасные (тип B ) и совсем не опасные (тип C ). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A . Стопка считается безопасной, если она не является взрывоопасной.

Для заданного количества контейнеров $N$ определить число безопасных стопок.

На вход программе подаётся одно число $1 \leqslant N \leqslant 10^5$.

Программа должна вывести одно число — количество безопасных вариантов формирования стопки, взятое по модулю $10^9+7$.

F: Поход вдоль реки

Дети пошли в поход вдоль реки. Поход начинается на левом берегу, заканчивается на правом. Дана последовательность букв ‘L’, ‘R’, ‘B’, означающая с какой стороны в реку впадает приток: ‘L’ — слева (left), ‘R’ — справа (right), ‘B’ — с обеих сторон (both). Определить минимальное количество переправ, которое придётся сделать школьникам.

На вход программа получает строку, содержащую только символы R, L, B в произвольном порядке. Длина строки не превосходит $10^5$ символов.

Выведите одно целое число — минимальное количество переправ.

G: Гвоздики

В дощечке в один ряд вбиты гвоздики. Любые два гвоздика можно соединить ниточкой. Требуется соединить некоторые пары гвоздиков ниточками так, чтобы к каждому гвоздику была привязана хотя бы одна ниточка, а суммарная длина всех ниточек была минимальна.

В первой строке входных данных записано число $N$ — количество гвоздиков $(2 \leqslant N \leqslant 100)$. В следующей строке заданы $N$ неотрицательных целых чисел, не превосходящие $10000$ — координаты всех гвоздиков в порядке возрастания.

Выведите единственное число — минимальную суммарную длину всех ниточек.

H: Покупка билетов

За билетами на премьеру нового мюзикла выстроилась очередь из $N$ человек, каждый из которых хочет купить $1$ билет. На всю очередь работала только одна касса, поэтому продажа билетов шла очень медленно, приводя «постояльцев» очереди в отчаяние. Самые сообразительные быстро заметили, что, как правило, несколько билетов в одни руки кассир продаёт быстрее, чем когда эти же билеты продаются по одному. Поэтому они предложили нескольким подряд стоящим людям отдавать деньги первому из них, чтобы он купил билеты на всех.

Однако для борьбы со спекулянтами кассир продавала не более $3$-х билетов в одни руки, поэтому договориться таким образом между собой могли лишь $2$ или $3$ подряд стоящих человека.

Известно, что на продажу $i$-му человеку из очереди одного билета кассир тратит $A_i$ секунд, на продажу двух билетов — $B_i$ секунд, трех билетов — $C_i$ секунд. Напишите программу, которая подсчитает минимальное время, за которое могли быть обслужены все покупатели.

Обратите внимание, что билеты на группу объединившихся людей всегда покупает первый из них. Также никто в целях ускорения не покупает лишних билетов (то есть билетов, которые никому не нужны).

На вход программы поступает сначала число $N$ — количество покупателей в очереди $(1 \leqslant N \leqslant 5000)$. Далее идет $N$ троек натуральных чисел $A_i, B_i, C_i$. Каждое из этих чисел не превышает $3600$. Люди в очереди нумеруются, начиная от кассы.

Требуется вывести одно число — минимальное время в секундах, за которое могли быть обслужены все покупатели.

I: Калькулятор с восстановлением ответа

Имеется калькулятор, который выполняет три операции:

• 1. прибавить к числу $X$ единицу;
• 2. умножить число $X$ на $2$;
• 3. умножить число $X$ на $3$;

Определите кратчайшую последовательность операций, необходимую для получения из числа $1$ заданное число $N$ $(1 \leqslant N \leqslant 10^6)$.

Выведите строку, состоящую из цифр 1 , 2 или 3 , обозначающих одну из трех указанных операций, которая получает из числа $1$ число $N$ за минимальное число операций. Если возможных минимальных решений несколько, выведите любое из них.

Источник

Входной файл	Выходной файл