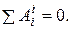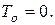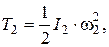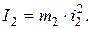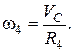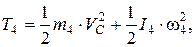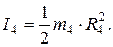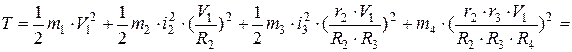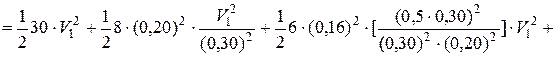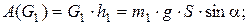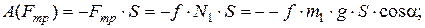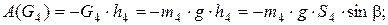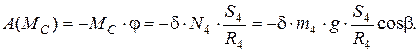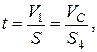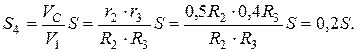Шкив с моментом инерции имеет две цилиндрические ступени
Вопрос по физике:
Шкив с моментом инерции ℑ имеет две цилиндрические ступени
радиусами R1 и R2. На цилиндры намотаны в противоположных на-
правлениях нити с грузами массой m1 и m2 на концах. Угловое уско-
рение шкива равно β, причем β > 0, если груз массой m1 опускается.
Определите неизвестную величину.
Дано:
R1=19,0 см
R2=27,0 см
m1=0,50 кг Решение пришлите фотографией )
m2=0,75 кг Заранее спасибо )
β=-1,2 рад/с^2
Найти
ℑ = ? кг⋅м^2
Ответы и объяснения 1
ℑ*β=M1-M2 — уравнение движения тела вокруг оси вращения
M1=m1*g*R1 — момент силы тяжести первого тела относительно оси
M2=m2*g*R2 — момент силы тяжести второго тела относительно оси
ℑ*β=m1*g*R1-m2*g*R2
ℑ*β=g*(m1*R1-m2*R2)
ℑ=g*(m1*R1-m2*R2)/β=10*(0,5*0,19-0,75*0,27)/(-1,2) кг⋅м^2=0,8958(3) кг⋅м^2
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Источник
Пример выполнения задания Д3
Условие задачи: решить 777 вариант задачи Д3. Запишем условие задачи в кратком виде (из таблиц Д-3.1 и Д-3.2):
1. Для решения задачи воспользуемся теоремой об изменении кинетической энергии механической системы:
(1)
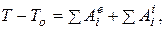
где: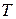 
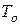
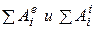
— кинетическая энергия механической системы в конечный момент времени, т.е. кинетическая энергия системы в момент, когда пройденный грузом 1 путь равен S;
— кинетическая энергия механической системы в начальный момент времени;
— сумма работ всех внешних и внутренних сил, приложенных к точкам механической системы, соответственно.
Рассматриваем предложенную механическую систему состоящую из абсолютно твердых тел связанных между собой недеформируемыми (нерастяжимыми) нитями. В этом случае сумма работ всех внутренних сил
По условию задачи механическая система в начальный момент времени находилась в состоянии покоя, следовательно:
Уравнение (1) принимает вид:
(2)
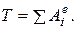
2. Определение кинетической энергии механической системы.
Кинетическая энергия механической системы равна сумме кинетических энергий всех тел, образующих систему, т.е.:
(3)
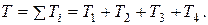
Кинетическая энергия твердого тела зависит от вида движения данного тела.
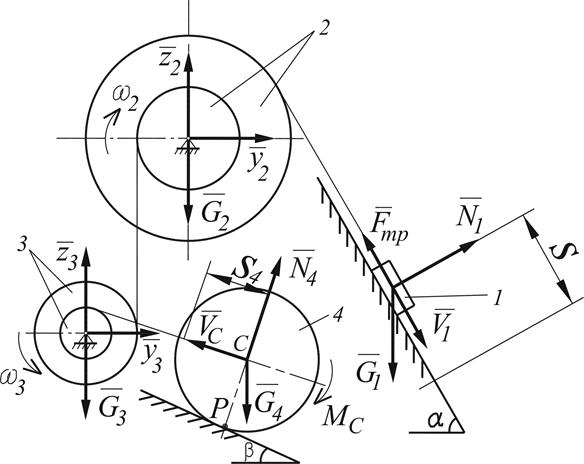
Предположим, груз 1 механической системы опускается по наклонной плоскости. В момент, когда пройденный им путь станет равным S, его скорость будет V1 . Груз 1, как следует из рис. Д3.2, совершает поступательное движение и его кинетическая энергия равна:
(4)
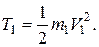
Ступенчатый шкив 2 совершает вращательное движение с угловой скоростью ω2 . Его кинетическая энергия равна:
где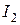 
— момент инерции ступенчатого шкива относительно оси вращения.
Момент инерции ступенчатого шкива:
(5)
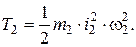
Ступенчатый шкив 3, так же как и тело 2, совершает вращательное движение вокруг неподвижной оси с угловой скоростью ω3 . Его кинетическая энергия равна:
(6)
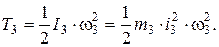
Каток 4 совершает плоское движение. Его центр масс т.С движется со скоростью VС . Пренебрегая проскальзыванием катка будем считать точку касания катка с наклонной плоскостью (т.Р) мгновенным центром скоростей, вокруг которого в данный момент времени вращается каток с угловой скоростью
Кинетическая энергия катка:
где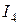 
— момент инерции катка относительно оси, проходящей через центр масс катка.
Полагая каток однородным цилиндром, найдем значение указанного момента инерции:
(7)
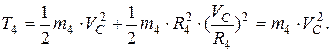
Подставим выражения (4), (5), (6) и (7) в уравнение (3):
(8)
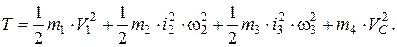
Установим зависимости между линейными и угловыми скоростями, выразив эти параметры через скорость груза 1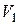 
.
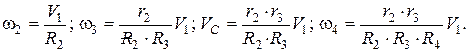
(9)
Подставим выражения (9) в уравнение (8) и упростим:
(10)
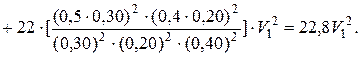
3. Найдем сумму работ всех внешних сил, приложенных к точкам механической системы, за время, когда груз 1 пройдет путь S. Покажем на рис. Д3.2 все внешние силы: силу тяжести груза 1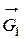 
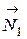
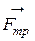
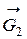
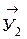
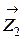
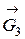
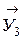
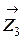
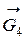
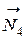
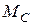
, нормальную реакцию 
, силу трения 
, силу тяжести блока 2 
и реакции подшипников 
и 
, силу тяжести блока 3 
и реакции подшипников 
и 
, силу тяжести катка 4 
, нормальную реакцию 
и момент сопротивления вследствие трения качения катка об опорную поверхность 
.
Помним, что работа силы равна нулю, если:
1) сила перпендикулярна перемещению тела;
2) сила приложена к неподвижной точке.
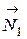
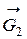
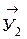
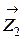
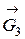
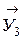
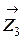
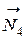
Учитывая это, видим, что работа сил , , , , , , и равна нулю.
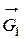
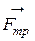
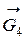
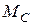
Таким образом, работу совершают силы , , и момент . Вычислим работу этих сил и момента:
а) работа силы тяжести :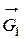
б) работа силы трения :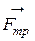
в) работа силы тяжести :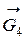
г) работа момента :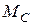
Соотношение между перемещениями S и S4 найдем из тех соображений, что за одно и то же время t:
Н·м = 109 Дж (10)
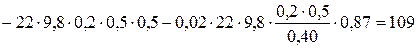
4. Приравниваем выражение (10) и (11) и находим искомую скорость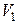 
:
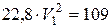
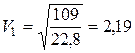
Дж,
м/с.
Скорость груза 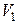положительна. Это означает, что наше предположение, будто груз 1 опускается, оказалось правильным.
5. Находим скорость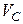 
:
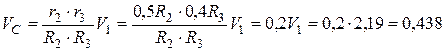
м/с.
ЛИТЕРАТУРА
1. Яблонский А.А. Курс теоретической механики. Часть II. Динамика. М., 1984. – 430 с.
2. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. М., 1983. – 575 с.
3. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Часть II. Динамика. М., 1964. – 663 с.
4. Лук’янець О.Г., Євдокімов А.І., Калашнікова Т.Г., Татаренко К.О., Нестеренко Т.П. Методичний посібник (довідник) з теоретичної механіки для виконання завдань розрахунково-графічних робіт №5 і №6 (розділ «Динаміка»). Макіївка: ДонНАБА, 2008. – 32 с.
5. Мущанов В.П., Євдокімов А.І., Лук’янець О.Г., Калашнікова Т.Г. Термінологічний довідник (посібник) з теоретичної механіки для використання в навчальному процесі при вивченні курсу «Теоретична механіка». Макіївка, ДонНАБА, 2008. – 30с.
6. Мущанов В.П., Загребельний М.І., Лук’янець О.Г. Методичні вказівки для самостійної роботи студентів з курсу «Теоретична механіка» (Розділ «Динаміка»). Розрахунково-графічна робота РР4. Макіївка: ДонНАБА, 2008. – 35с.
7. Тарг С.М. Краткий курс теоретической механики. М., 1986.
Источник