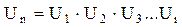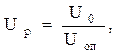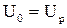Разбивка передаточных отношений по ступеням

Разбивка передаточного отношения по ступеням

Разбивка передаточного отношения по ступеням

• Разбивка передаточного числа При проектировании многоступенчатой ​​передачи возникают проблемы оптимального выбора количества ступеней и распределения передаточных чисел по ступеням. Решение этой проблемы зависит от требований к передаче. Не существует унифицированного решения для конструкций, используемых для малой мощности, измерительных приборов и снижения мощности. Наиболее важным в приборостроении является минимизация размеров, массы, скорости или инерции и минимизация ошибок передачи.

Условия, которые минимизируют размеры. При равных передаточных числах расстояние между приводом и выходным валом минимально. ’12 = ’23 = … = ‘ Людмила Фирмаль

Условия минимизации массы. Оптимальное количество шагов в зависимости от условий (14,5) «Опт = 3 Джиу. (14,6) Поскольку уменьшение количества шагов повышает эффективность передачи, рекомендуется округлить значение, полученное в уравнении (14.6), до более низкого целочисленного значения. Оптимальное передаточное число для этапа составляет 2,16. Условия минимизации уменьшения момента инерции. Использование низкоинерционных передач ускоряет работу механизма в режиме пуска / останова и обеспечивает стабильность системы слежения.

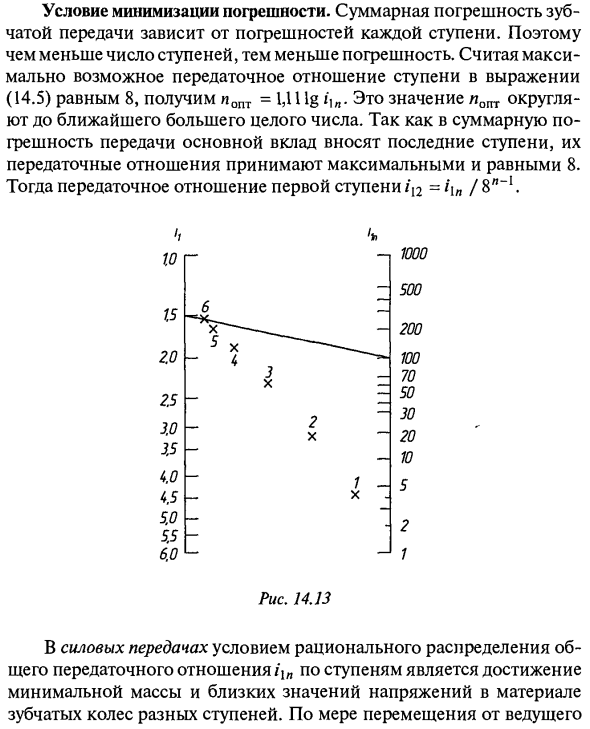
Момент инерции механизма минимизируется за счет минимального веса и габаритов колеса. Низкооборотное шаговое колесо мало влияет на момент инерции. Поэтому рекомендуется уменьшить передаточное число высокоскоростной ступени. Колеса легко нагруженной скоростной ступени должны быть изготовлены из пластика. Оптимальное количество шагов определяется уравнением (14.6). Используйте номограмму, показанную на рисунке, чтобы найти приблизительное передаточное число для каждой ступени в 14.13. Передаточное число для первой ступени / 12 определяется следующим образом.

• На правой вертикальной шкале номограммы найдите раздел, соответствующий общему передаточному отношению / 1 л. Затем проведите прямую линию через этот сегмент и точку, помеченную крестиком, который соответствует общему количеству шагов. Пересечение этой прямой с левой вертикальной шкалой указывает передаточное число первой ступени / 12. Например, для f1 = 100 и lopt = 6 мы решили, что f12 = 1.5 (рисунок 14.13). Передаточное число последующей ступени in_x составляет i 1ya / / 12. Затем в правой вертикальной шкале найдите сегмент, который соответствует передаточному отношению ступени, и нарисуйте прямую линию, которая проходит через точку, соответствующую этому сегменту, и крест, обозначенный шагом -1.

Общая ошибка передачи зависит от ошибки каждой ступени. Следовательно, чем меньше количество шагов, тем меньше ошибок. Если максимально возможное передаточное число в уравнении (14.5) равно 8, iopt = 1,11 log /, „. Это значение лопасти округляется до ближайшего целого числа. Последний шаг вносит существенный вклад в общую ошибку передачи. Максимальное передаточное число равно 8. Передаточное число первой ступени равно / | 2 = i \ n / 8π’1. Рисунок 14.13 В устройстве передачи энергии разумным условием распределения ступенчатого общего передаточного числа iXn является достижение значения напряжения, близкого к минимальной массе материала зубчатой ​​передачи для различных ступеней.

Пересечение этой прямой и левой вертикальной шкалы указывает передаточное число второй ступени. Людмила Фирмаль

При переходе от ведущего звена редуктора к выходу частота вращения уменьшается, а крутящий момент увеличивается. Чтобы уменьшить натяжение зубьев зацепления, увеличьте ширину колеса медленного шага. Передаточное число высокоскоростной ступени может увеличивать передаточное число тихоходной, чтобы приблизить массу колеса.

Если вам потребуется заказать решение по прикладной механике вы всегда можете написать мне в whatsapp.

Источник

Разбивка передаточного отношения по ступеням

При проектировании многоступенчатых передач возникает задача оптимального выбора числа ступеней и распределения передаточного отношения по ступеням. Решение этой задачи зависит от требований, предъявляемых к передаче. Единых решений при проектировании маломощных, используемых в приборостроении, и силовых редукторов нет.

В приборостроении наиболее важными являются требования по минимизации габаритов и массы; по быстродействию, т.е. минимизации инерционности; по минимизации погрешности передачи. Рассмотрим влияние отдельных требований и условий, предъявляемых к передачам.

Условие минимизации габаритов. Величина межосевого расстояния между ведущим и выходным валами будет минимальной при равенстве передаточных отношений ступеней

i₁₂ = i₂₃ = … = i_(n–1)n = 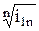, (14.10)

где i_1n – общее передаточное отношение многоступенчатой передачи; n – число ступеней.

Между оптимальным числом ступеней и общим передаточным отношением имеется зависимость

Как показали исследования, оптимальное для каждой ступени передаточное отношение равно 3,5.

Условие минимизации массы.Оптимальное число ступеней при сохранении зависимости (14.10) равно

Полученную по формуле (14.12) величину рекомендуют округлять до меньшего целого значения, так как с уменьшением числа ступеней растет КПД передачи. Оптимальное значение передаточного отношения ступени составит 2,16.

Условие минимизации приведенного момента инерции.Использование малоинерционных передач позволяет увеличить быстродействие механизма, работающего в стартстопном режиме и обеспечить устойчивость работы следящих систем. Момент инерции механизма будет минимальным при минимальных массах и габаритах колес. Колеса тихоходных ступеней мало влияют на момент инерции. Поэтому рекомендуют передаточные отношения быстроходных ступеней принимать малыми, колеса малонагруженных быстроходных ступеней изготовлять из пластмасс.

Оптимальное число ступеней определяют по формуле (14.12). С помощью номограммы, представленной на рис. 14.13, находят ориентировочно передаточные отношения отдельных ступеней. Передаточное отношение первой ступени i₁₂ определяют следующим образом. На правой вертикальной шкале номограммы находят деление, соответствующее общему передаточному отношению i_1n. Затем проводят прямую через это деление и точку, обозначенную крестиком, соответствующую общему количеству ступеней. Точка пересечения этой прямой с левой вертикальной шкалой покажет передаточное отношение первой ступени i₁₂. Например, при i_1n =100 и n_опт = 6 определили (рис. 14.13), что i₁₂ =1,5.

i1n

Передаточное отношение последующих i_n-1 ступеней равно i_1n/i₁₂. Далее на правой вертикальной шкале находят деление, соответствующее передаточному отношению i_n–1 ступеней и проводят прямую через это деление и точку, обозначенную крестиком, соответствующую (n – 1) ступеней. Точка пересечения этой прямой с левой вертикальной шкалой покажет передаточное отношение второй ступени i₂₃ и т.д.

Условие минимизации погрешности.Суммарная погрешность зубчатой передачи зависит от погрешностей каждой ступени. Поэтому чем меньше число ступеней, тем меньше погрешность. Считая максимально возможное передаточное отношение ступени в выражении (14.10) равным 8, получим

Полученное значение n_опт округляют до ближайшего большего целого значения. Так как в суммарную погрешность передачи основной вклад вносят последние ступени, принимают их передаточные отношения максимальными и равными 8. Тогда передаточное отношение первой ступени будет равно i₁₂ = i_1n/8 n –1 .

В силовых передачахусловиями рационального распределения общего передаточного отношения i_1n по ступеням являются достижение минимальной массы и близких значений напряжений в материале зубчатых колес разных ступеней. По мере перемещения от ведущего звена редуктора к выходному уменьшается скорость вращения и увеличивается вращающий момент. Для уменьшения напряжений зубьев в зацеплении увеличивают ширину колес тихоходных ступеней. Для получения близких диаметров колес передаточное отношение быстроходных ступеней можно принимать больше передаточных отношений тихоходных.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Определение передаточного отношения привода и его разбивка по ступеням передач.

Общее передаточное отношение привода определяется по формуле

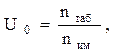
С другой стороны, передаточное отношение многоступенчатой передачи может быть получено перемножением передаточных отношений отдельных ступеней передач:

где Ui – передаточное отношение отдельной i-й ступени передач,

n – число ступеней передач по кинематической схеме.

Примем обозначения передаточных отношений: U_оз – открытая зубчатая передача; U_ц – цепная передача; U_рм – ременная передача.

Если по кинематической схеме передач редуктора имеется открытая передача (зубчатая, цепная или ременная), то, принимая по табл. 4.4 передаточное отношение открытой передачи, находят передаточ­ное отношение редуктора:

где U_оп – передаточное отношение отрытой передачи.

Если открытой передачи в приводе нет (схема 1, рис. 1), то 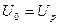. После определения общего передаточного отношения редуктора производится его разбивка по отдельным ступеням передач. В случае стандартного редуктора разбивка по ступеням не производится, а

Передаточ­ные отношения одноступенчатых цилиндрических и конических редукто­ров, проектируемых для серийного производства, выбираются из ря­дов:

1-й ряд	2,0	2,5	3,15	4,0	5,0	6,3	12,5
2-й ряд	2,24	2,8	3,55	4,5	5,6	7,1	11,2	—

Предпочтительнее 1-й ряд. Для одноступенчатых редукторов (за исключением червячных и волновых) не рекомендуется брать более:

Umax = 6,3 — для конических передач;

Umax = 8 — для цилиндрических передач;

Umax = 12,5 — для планетарных передач.

При больших значениях Up принимают число ступеней передач больше единицы или, если это возможно, применяют более тихоходный двигатель.

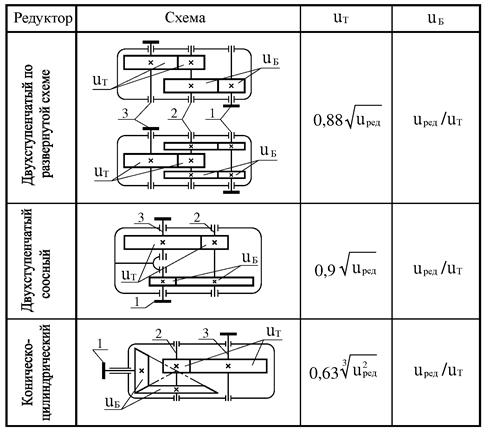
Передаточное отношение тихоходной – Uт и быстроходной – Uб ступеней двухступенчатых редукторов можно определить таблице 4.4.

Таблица 4.4 – разбивка передаточного отношения по ступеням редуктора

Примечание. На приведенных в таблице схемах редукторов обозначено:

1 — входной вал; — промежуточный вал; — выходной вал.

Точность разбивки общего передаточного отношения проверяется следующим условием:

Источник

Разбивка передаточных отношений по ступеням

Передаточные числа одноступенчатых передач приведены в табл. 5.5. В многоступенчатых передачах и в редукторах передаточное число следует разбить по ступеням. От разбивки общего передаточного числа по ступеням в двух- и трехступенчатых редукторах (а также в коробках передач) в значительной степени зависят удобство смазывания колес и компоновки деталей, а также конструкция корпуса и его габариты.

Универсальных рекомендаций по разбивке передаточного числа по ступеням, удовлетворяющих всем указанным условиям, не существует. Выбор способа разбивки передаточного числа зависит от конкретных требований, которым должна отвечать конструкция: обеспечения минимальных габаритов редуктора и минимальной массы зубчатых колес, получения одинакового погружения зубчатых колес всех ступеней в масляную ванну, создания наименьшей установочной площади корпуса редуктора и др. [15].

В основу решения задачи о разбивке передаточного числа иногда кладут условие полного использования нагрузочной способности всех ступеней редуктора [5]. Стандартные передаточные числа для цилиндрических одно-, двух- и трехступенчатых редукторов и их разбивка по ступеням приведены в табл. 5.6 (механические характеристики материалов всех колес примерно одинаковы). В соосных редукторах иногда где — коэффициенты ширины колес соответственно тихоходной и быстроходной ступеней.

В коническо-цилиндрических редукторах принимают такие же значения передаточных чисел, как и в цилиндрических многоступенчатых (см. табл. 5.6). В зубчато-червячных редукторах для

зубчатой пары принимают передаточное число не выше 2. 2,5 (при этом получается удобная компоновка деталей в корпусе). В червячно-зубчатых редукторах для зубчатой пары принимают передаточное число

Для двухступенчатых червячных редукторов удобство компоновки требует обеспечения где и — межосевые расстояния тихоходной и быстроходной ступеней. При этом передаточные числа тихоходной и быстроходной ступеней получаются примерно равными

Когда частота вращения ведомого вала должна иметь не одно, а несколько конкретных значений, применяют коробки передач, которые обеспечивают ступенчатое изменение передаточных чисел. При проектировании коробок передач часто принимают ряды частот вращения валов в виде геометрической прогрессии со знаменателями . Тогда частоты вращения валов будут:

Источник