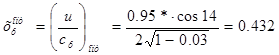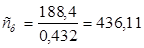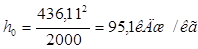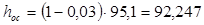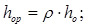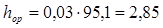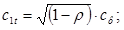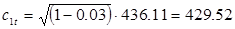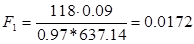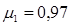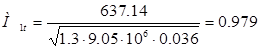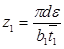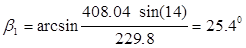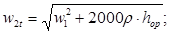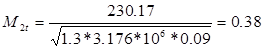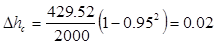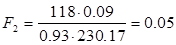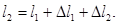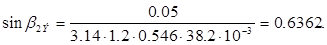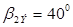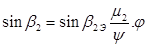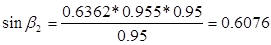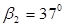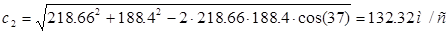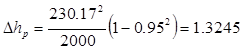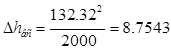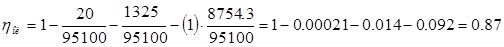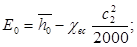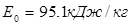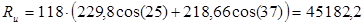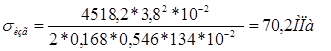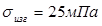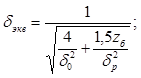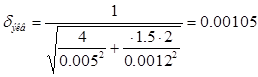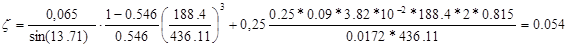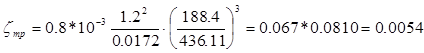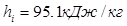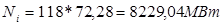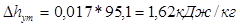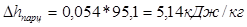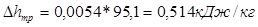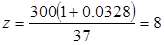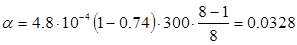Расчет последней ступени паровой турбины

Расчет турбинных ступеней. Методика расчета турбинной ступени

Главная > Лекция >Промышленность, производство

Лекция №8. Расчет турбинных ступеней

8.1. Выбор исходных данных и параметров при расчете турбинной ступени

При расчете турбинной ступени устанавливают форму проточной части сопловых и рабочих решеток, определяют их размеры, шаг расположения лопаток в соответствующих решетках, углы их установки, а также выбирают конструкции надбандажных и диафрагменных уплотнений. Перед расчетом ставятся две основные задачи : 1. получение высокой экономичности турбинной ступени; 2. обеспечение требуемой надежности всех ее элементов. Оценка экономичности ступени осуществляется по рассчитанному значению ее относительного внутреннего КПД. Итогом расчета является определение внутренней мощности ступени.

Исходными данными для расчета являются следующие величины: расход водяного пара G , кг/с; его термодинамические параметры р 0 , МПа, t 0 , 0 С; скорость потока на входе в ступень с 0 , м/с и ее направление (угол  0 ). Известными также являются средний диаметр d ср , м и частота вращения ротора турбины n , с -1 .

Предварительно оценивается степень реактивности ступени в зависимости от ее типа (активного или реактивного), места расположения в проточной части турбины (первые, промежуточные или последние ЦВД, ЦСД, ЦНД). Обычно первая ступень ЦВД турбин с сопловым способом парораспределения является регулирующей (парциальной) и выполняется активного типа (  =0,02…0,08) , а последние ступени конденсационных турбин проектируются с высокой степенью реактивности. В турбинах активного типа промежуточные ступени выполняются со степенью реактивности  =0,10…0,35 . При этом, чем меньше отношение d / l решеток турбинной ступени, тем большим выбирается значение ее степени реактивности. В представляемой далее методике расчета ступеней с лопатками постоянного профиля вычисление степени реактивности на среднем диаметре можно проводить по упрощенной формуле

Значение степени реактивности в корневом сечении ступени принимается равным  кор =0,03…0,05 (  кор =0,1…0,3 для последних ступеней ЦНД). Следует помнить, что от ступени к ступени с ростом степени реактивности в сечении по среднему диаметру увеличивается оптимальное отношение скоростей u /с ф в соответствии с формулой

На рис. 8.1 представлена схема ступени активного типа, в рабочей решетке которой основная часть располагаемого теплоперепада приходится на сопловую решетку. Для реактивных ступеней улучшается обтекание лопаток рабочей решетки за счет большей конфузорности ее межлопаточных каналов, что способствует росту относительного лопаточного КПД  ол . Но за счет увеличенного теплоперепада в рабочей решетке (соответственно и большей разности давлений р 1 -р 2 ) растут протечки через зазоры уплотнений, а также осевые нагрузки, действующие как на рабочие лопатки, так и на диск ступени. В общем случае, с повышением степени реактивности турбинных ступеней уменьшаются оптимальные значения их теплоперепадов , что приводит к росту числа ступеней турбины и ее стоимости. Обычно выбор степени реактивности является технико-экономической задачей и осуществляется в процессе оптимизации всей проточной части паровой турбины.

Рис. 8.1. Фрагменты проточной части межлопаточных каналов турбинной ступени

В зависимости от выбранной степени реактивности оценивается оптимальное отношение скоростей u /с ф , обеспечивающее максимальные значения  ол и  о i . Выбор параметра u /с ф  ( u /с ф ) опт позволяет при том же значении окружной скорости u реализовывать больший теплоперепад Н 0 в ступени и тем самым сократить их количество в турбине. Ранее были даны следующие рекомендации по связи параметров  и u /с ф :

при  =0-0,1 u /с ф =0,46…0,5; при  =0,1-0,2 u /с ф =0,51…0,53; при  =0,5 u /с ф =0,55…0,65.

8.2. Методика расчета турбинной ступени c  = d / l  10…13

Данная методика расчета предполагает, что течение в сопловой и рабочей решетках ступени может считаться плоскопараллельным и параметры потока водяного пара по высоте решеток сохраняются постоянными < р 1 ( r )= const , c 1 ( r )= const ,  1 ( r )= const >. Это предположение оправдано при расчете ступеней с d / l  10…13 , т.е. для относительно коротких лопаток первых ступеней ЦВД паровых турбин. В этом случае расчет осуществляется по среднему диаметру ступени d ср , значение которого известно. Выбрано также значение степени реактивности ступени  . Основные этапы расчета следующие:

Производится оценка скорости потока на входе в ступень с 0 ( с 0 =0 м/с для первой ступени отсека турбины и с 0 0 для промежуточных ступеней) и угла  0 (  0 90 0 ).

Принимается значение коэффициента использования энергии с выходной скоростью  вс (для регулирующей ступени и последних ступеней отсеков и цилиндров турбины  вс =0, а для промежуточных ступеней  вс 0,8…1).

Задается эффективный угол выхода  1Э с учетом того, что уменьшение его значения приводит к росту высоты лопаток и КПД ступени. Обычно для ступеней активного типа принимают значение эффективного угла из диапазона  1Э =11…16 0 .

Осуществляется предварительная оценка относительной хорды профиля сопловой решетки b 1 / l 1 . Обычно для активных ступеней b 1 =40…80 мм (см. табл. 7.1), а для реактивных — b 1  b 2 =20…60 мм. При выполнении типового расчета рекомендуется принять значения b 1 =60 мм и b 2 =30 мм. Высоту лопаток оценивают по результатам расчета предыдущих ступеней, а для первой ступени с короткими лопатками необходимо выполнять условие l 1 10..12 мм (для регулирующей ступени мощных турбин 20-25 мм).

На основе выражения (4.13) или по данным рис. 6.7 оценивается значение коэффициента скорости сопловой решетки  .

По формуле (5.12) вычисляется оптимальное отношение скоростей ( u /с ф ) опт и принимается решение о выборе значения параметра u /с ф для рассчитываемой ступени (для ряда ступеней определяющими факторами при выборе значения u /с ф являются необходимость срабатывания больших теплоперепадов.).

После определения окружной скорости u =  d ср n вычисляется значение фиктивной скорости с ф = u /( u /с ф ).

Далее вычисляется располагаемый теплоперепад ступени по параметрам полного торможения рабочей среды: , Дж/кг. В тех случаях, когда располагаемый теплоперепад турбинной ступени известен (в типовом расчете следует принять располагаемый теплоперепад регулирующей ступени из диапазона 60-80 кДж/кг), то оценивается значение u /с ф .

Определяются изоэнтропийный теплоперепад сопловой решетки по параметрам торможения и располагаемый теплоперепад рабочей решетки .

Осуществляется вход в h , s — диаграмму, с помощью которой по известным параметрам торможения водяного пара и находится значение энтальпии (рис. 7.10) и далее с учетом энергии входной скорости потока в ступень 0,5с с 2 вычисляется энтальпия h 0 = -0,5с с 2 (энтальпия по статическим параметрам водяного пара р 0 , t 0 ) Далее, для условий изоэнтропийного расширения водяного пара в сопловой решетке, определяется значение энтальпии h 1 t = — , по которому в h , s — диаграмме находится статическое давление р 1 среды за сопловой решеткой (рис. 7.10). Здесь же, в точке « 1 t » для теоретического процесса расширения, находится значение удельного объема v 1 t , м 3 /кг .

Рис. 7.10 (повтор). Процесс расширения водяного пара в турбинной ступени

Теоретическая скорость потока на выходе из сопловой решетки позволяет оценить число Маха М 1 t =с 1 t /а 1 t , где скорость звука а 1 t = . Для перегретого водяного пара значение показателя изоэнтропы х =1,3.

Для дозвукового режима течения пара в межлопаточных каналах сопловой решетки ( М 1 t 1) значение площади ее горловых сечений F 1 определяется из уравнения неразрывности , где коэффициент расхода  1 оценивается по выражению (6.4) или на основе данных рис. 6.6, а (в первом приближении  1 0,97).

Для сверхзвукового режима ( М 1 t 1) обычно применяют суживающие по форме каналы сопловой решетки, но ее выходная площадь находится по критическим значениям скорости и удельного объема. Они вычисляются по критическому отношению давлений , значение которого для перегретого водяного пара   =0,546. Тогда, определив р 1  , с помощью h , s – диаграммы (рис. 8.3) находится критический теплоперепад и значение критической скорости .

Рис. 8.3. К определению критических значений термодинамических параметров

Источник

Курсовая работа: Тепловой расчет паровой турбины

Тепловой расчет турбины выполняется с целью определения основных размеров и характеристик проточной части: числа и диаметров ступеней, высот их сопловых и рабочих решеток и типов профилей, к.п.д. ступеней, отдельных цилиндров и турбины в целом. Тепловой расчет турбины выполняется на заданную мощность, заданные начальные и конечные параметры пара, число оборотов; при проектировании турбины с регулируемыми отборами пара, кроме того, на заданные давления и величину отборов. В данном курсовом проекте произведен тепловой расчет турбины Р-40-130/31.Даны все нужные исходные данные. Целью курсового проектирования является закрепление, расширение и углубление теоретических знаний по дисциплине “Паровые и газовые турбины”. Курсовой проект включает проведение большого объёма расчётных работ, поэтому при его выполнении нужно максимально использовать ЭВМ, что существенно повысит качество проекта.

Паровая турбина является двигателем, в котором потенциальная энергия перегретого пара преобразуется в кинетическую энергию и , затем в механическую энергию вращения ротора.

Для турбин типа Р за расчетный расход пара принимается расход пара на турбину при режиме номинальной мощности.

1.1 Построение рабочего процесса турбины и определение расхода пара на турбину

Процесс расширения начинают строить с состояния пара перед стопорным клапаном турбины (рис.1) определяемого начальными параметрами P 0 , t 0 . Состояние пара перед соплами первой ступени определяют с учётом его дросселирования в клапанах

P’ 0 = (0,96)·P 0 =0,96*12,75=11,97 МПа

Название: Тепловой расчет паровой турбины Раздел: Промышленность, производство Тип: курсовая работа Добавлен 09:12:16 04 января 2011 Похожие работы Просмотров: 10631 Комментариев: 14 Оценило: 6 человек Средний балл: 4 Оценка: 4 Скачать

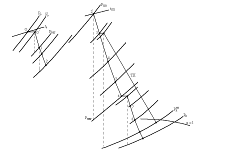Рисунок 1- Процесс расширения пара в турбине с промперегревом в i-s–диаграмме

Внутренний КПД регулирующей ступени и отдельных частей турбины принимается по аналитическим зависимостям или по опытным данным, полученным в результате испытаний однотипных турбин.

Для турбин с n = 50 сек -1 КПД регулирующей ступени зависит в основном от площади сопловой решётки, пропорциональной объёмному расходу пара.

В турбинах типа Р в качестве регулирующей ступени устанавливают до мощности 40 МВт включительно как одновенечные, так и двухвенечные ступени, выше 50 МВт – одновенечные. Одновенечные — h_о рс =95 кДж/кг.

Располагаемый теплоперепад в турбине определяем по формуле:

От точки Р_о / по изоэнтропе откладывается выбранный тепловой перепад на регулирующую ступень h_о рс (рис.3.1). Изобара Р₂ рс , проведенная через точку С конца отрезка h_о рс , соответствует давлению за регулирующей ступенью. Для того, чтобы на этой изобаре найти точку начала процесса в нерегулируемых ступенях, необходимо учесть потери в регулирующей ступени.

КПД одновенечной регулирующей ступени можно найти по формуле

(1)

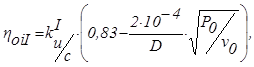
где k u /с — коэффициент, учитывающий отклонение отношения скоростей u/с ф от оптимального значения;

Р 0 ,v 0 — давление, Па, и удельный объём, м³/кг, перед соплами регулирующей ступени;

D — расход пара через ступень, кг/с.

Величину D можно принять равной расходу пара на турбину, найденному для её прототипа или приближённо оценить из выражения

(2)

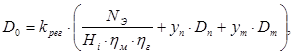
где k_рег – коэффициент регенерации, учитывающий увеличение расхода пара из-за регенеративных отборов, k_рег =1,15…1,30;

Н i – действительный теплоперепад конденсационного потока пара;

η_м , η_г – механический КПД турбины и КПД электрогенератора, принимаемые для турбин мощностью более 50 МВт, соответственно 0,99 и 0,997;

D_п , D_т – расходы пара на производственные нужды и теплофикацию;

y_п , y_т – коэффициенты недовыработки мощности паром промышленного и отопительного отборов.

КПД групп ступеней ЧНД, работающих на перегретом пареКак правило, наибольшее значение имеет КПД ЧСД турбины, где высота лопаток достигла значительной величины, нет регулирующей ступени и отсутствуют потери энергии от влажности.

Расход пара на ЦНД:

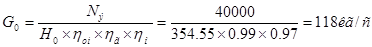Т.к. ЦНД выполнен однопоточным, то расход пара на один поток G₁ = 118 кг/с.

1.2 Выбор и расчёт регулирующей ступени

Первая ступень в турбинах с сопловым парораспределением работает с переменной парциальностью при изменении расхода пара и называется регулирующей. В турбинах с дроссельным парораспределением регулирующая ступень отсутствует.

В качестве регулирующей ступени может быть использована одновенечная ступень или двухвенечная ступень скорости. Выбор типа регулирующей ступени производится с учетом ее влияния на конструкцию и экономичность турбины. Использование теплоперепад в одновенечной (80…120 кДж/кг), что приводит к сокращению числа нерегулируемых ступеней и снижению металлоемкости и стоимости турбины. При этом уменьшится температура и давление пара перед нерегулируемыми ступенями, а это позволит применить более дешевые, низколегированные стали для их изготовления, снизить утечки пара через переднее концевое уплотнение и увеличить высоту лопаток первой нерегулируемой ступени. Расчет регулирующей ступени сводится к определению ее геометрических размеров, выбору профилей сопловых и рабочих лопаток, нахождению мощности и КПД ступени. Поскольку характеристики этой ступени оказывают существенное влияние на конструкцию, число ступеней и КПД всей турбины, то необходимо стремиться спроектировать эту ступень с высоким КПД. Исходными данными для расчета регулирующей ступени являются частота вращения ротора турбины, расход пара на турбину и параметры пара перед ступенью. В качестве определяющего размера принимают средний диаметр ступени d. Расчет одновенечной регулирующей ступени (рис.2) производят в следующей последовательности.

Находят окружную скорость ступени 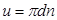и выбирают степень реактивности ρ на среднем диаметре в пределах 0,03-0,08. Такая величина ρ исключает возможность появления отрицательной реактивности у корня лопаток на нерасчетных режимах.

Рисунок 2 — Ступень турбины

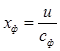
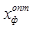
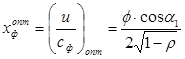
Большое влияние на характеристики ступени оказывает характеристический коэффициент . В первом приближении его можно принять равным , обеспечивающим максимум лопаточного КПД

, (3)

где 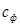— фиктивная скорость пара;

φ — коэффициент скорости сопловой решетки;

— угол выхода пара из сопловой решетки;

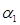
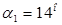
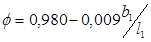
Предварительно можно принять , φ=0,95 с последующим уточнением по формуле

(4)

Действительное отношение 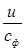рекомендуется принять меньше оптимального для увеличения теплоперепада на регулирующую ступень.

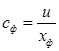
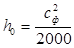
Фиктивная скорость на выходе из сопловой решетки позволяет определить располагаемый теплоперепад, срабатываемый в ступени .

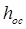
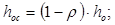
С учетом принятой степени реактивности ρ находят располагаемый теплоперепад в сопловой и рабочей решетках, а так же теоретическую скорость пара на выходе из сопел

(5)

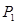
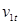
Отложив найденные теплоперепады в i-s-диаграмме (рис.3) находят давление и теоретический удельный объем за соплами, что позволяет определить выходную площадь сопловой решетки:

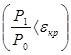
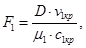
при сверхзвуковой скорости для суживающихся сопел

(6)

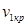
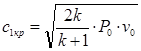
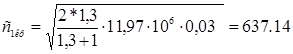
где: — удельный объем при критическом давлении;

-критическая скорость течения

— коэффициент расхода, принимаем предварительно равным 0,97, а затем уточняемый по формуле:

м/с (7)

Для перегретого пара k=1,3; .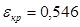

Рисунок 3 — Процесс расширения пара в регулирующей ступени

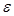
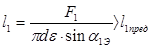
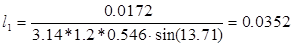
Задавшись предварительно степенью парциальности , определяют высоту сопловой решетки, которая должна быть больше предельно допустимой величины

(8)

м

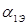
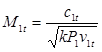
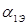
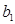
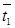
Длину лопатки можно увеличить уменьшая степень парциальности, угол или диаметр ступени. По числу Маха , углу и табл.1 выбирали профиль сопловых решеток, хорду профиля =50 мм, оптимальный относительный шаг =0,80 и определены число сопловых лопаток равно 49.

По геометрическим характеристикам профелей лопаток выбираем профиль сопловой решётки по таблице 1.

Профиль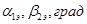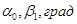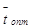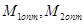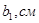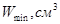

С – 90 – 15Б

13 – 17

70 – 120

0,70 – 0,85

0,85 – 1,15

5,2

0,413

(9)

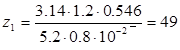
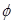
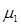
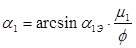
По формулам (4) и (7) уточняют значения коэффициентов , и угла

.

При их небольшом расхождении с принятыми ранее значениями расчет можно не повторять.

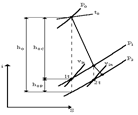
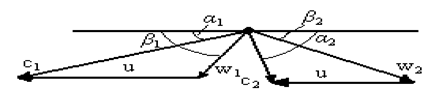
Строят входной треугольник скоростей (рис.4), для чего определяют действительную скорость пара на выходе из сопловой решетки

(10)

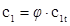
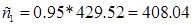Из треугольника находят относительную скорость входа пара на рабочую решетку и угол ее направления

(11)

м/с

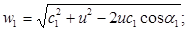
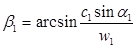
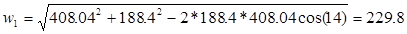
Теоретическая относительная скорость выхода пара из рабочей решетки и число Маха равны:

(12)

м/с

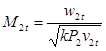
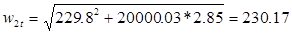
Рисунок 4 — Треугольники скоростей турбинной ступени

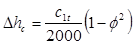
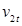
Откладывая потери энергии в соплах на i– s-диаграмме, строят действительный процесс расширения в них и определяют теоретический удельный объем пара в конце адиабатного расширения на рабочих лопатках.

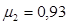
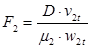
Предварительно задавшись коэффициентом расхода находим выходную площадь рабочей решетки определяем по формуле:

(13)

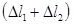
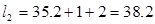
Выбрав суммарную перекрышу определяем высоту рабочей решетки

м

Эффективный угол выхода пара из рабочей решетки находят из выражения

(14)

=0,38

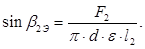
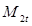
По геометрическим характеристикам профелей лопаток выбираем профиль рабочей решётки таблице 1.

Профиль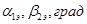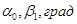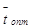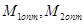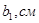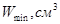

Р – 35 – 25А

22 – 28

30 – 50

0,55 – 0,65

до 0,85

2,54

0,168

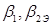
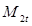
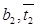
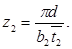
По углам и числу выбираем профиль рабочей решетки ее основные геометрические характеристики и определяют число лопаток

(15)

Уточняем коэффициент расхода и находим скоростной коэффициент рабочей решетки:

(16)

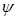
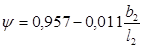
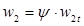
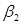
Производим построение выходного треугольника скоростей по и углу , найденному по формуле

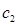
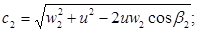
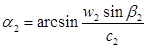
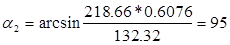
Из выходного треугольника находят абсолютную скорость выхода пара из ступени , угол ее направления α 2 , выбирают профили рабочих лопаток, по формуле:

(17)

0

Потери энергии в рабочей решетке и с выходной скоростью равны:

;(18)

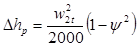
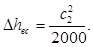
Откладывая значение 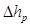в i-s — диаграмме, строят действительный процесс расширения пара в рабочих лопатках.

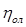
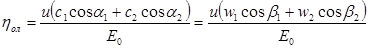
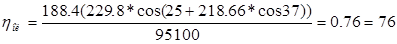
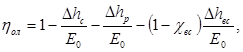
Относительный лопаточный КПД определим двумя способами:

(19)

%

(20)

где : Е₀ – располагаемая энергия ступени, кДж/кг;

χ_вс – коэффициент использования кинетической энергии выходной скорости в последующей ступени, для регулирующей ступени 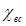= 0.

Для оценки прочностных характеристик рабочих лопаток находим изгибающие напряжения и сравнивают их с допустимыми значениями. Поскольку степень реактивности в регулирующей ступени не велика, можно ограничиться окружным усилием:

(21)

(22)

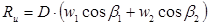
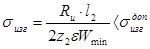
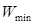
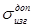
где: – минимальный момент сопротивления, определяемый по характеристике профиля. В ступенях с парциальным подводом =25 МПа.

Значения КПД, найденные по формулам (19) и (20) должны совпадать в пределах точности расчетов.

Мощность на лопатках ступени равна:

(23)

МВт

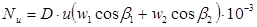
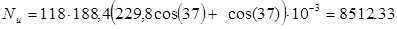
Определяют потери энергии от утечек пара, парциальности и на трение. Относительная величина потерь энергии от утечек пара через диафрагменные и бандажные уплотнения определяем по формуле:

(24)

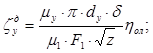
где :μ_у – коэффициент расхода уплотнения, μ _у = 0,9;

d_у – диаметр диафрагменного уплотнения, принимаемый по аналогу турбины, d_у = 0,5 м;

δ – радиальный зазор в уплотнении, δ ≈ 0,001d_у ;

z – число гребней уплотнения, в области низкого давлений будет z = 4;

м

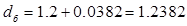
d_б – диаметр бандажного уплотнения,

δ_экв – эквивалентный зазор уплотнения

— осевой и радиальный зазоры бандажного уплотнения;

— число гребней в надбандажном уплотнении.

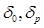
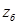
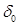
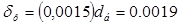
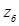
При проектировании ступени можно принять = 0,005м;

м , = 2.

Относительные потери энергии, вызванные парциальным подводом пара:

(25)

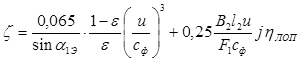
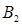
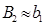
где: — ширина рабочей решётки, ;

j — число пар концов сопловых сегментов, чаще всего j = 2.

Потери энергии от трения диска о пар определяем по формуле:

(26)

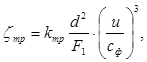
где: 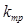— коэффициент трения, равный (0,8)10 -3 .

Относительный внутренний КПД ступени определяем по формуле:

(27)

=81,5%

=1,7%

=0,54%

%

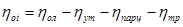
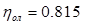
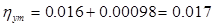
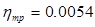
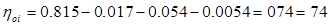
Использованный теплоперепад ступени определяем по формуле:

(28)

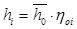
Внутренняя мощность ступени определим по формуле:

(29)

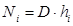
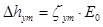
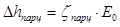
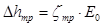
Откладывая последовательно потери энергии , , в i-s-диаграмме находят состояние пара за регулирующей ступенью.

1.3 Предварительный расчёт нерегулируемых ступеней

Расчёты нерегулируемых ступеней проводят в два этапа. На первом этапе проектирования определяют число ступеней, основные их размеры, теплоперепады и другие характеристики, по которым в целом оценивается будущая конструкция турбины. Она удовлетворяет поставленным требованиям, то выполняют детальный расчёт ступеней, в результате которого определяем окончательные характеристики турбины.

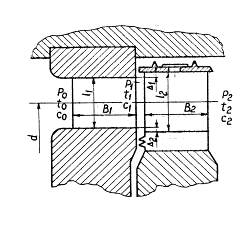
Прежде всего, оценивают размеры первой и последней нерегулируемых ступеней для каждого цилиндра турбины. Диаметр первой ступени ЦНД и ЦСД принимают с учётом конструктивных и технологических соображений, используя размеры изготовленных турбин. Высоту сопловых лопаток находим по формуле:

(30)

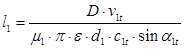
где: 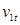— удельный объём в конце адиабатного расширения в сопловой решётке;

u/с_ф = 0,432; ρ = 0,03; ε =1; 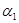= 14 0 .

Высота лопаток не должна быть меньше 15…20 мм. Диаметр последней ступени турбины находят из уравнения неразрывности для выходного сечения рабочей решётки определим по формуле:

(31)

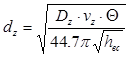
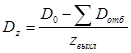
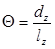
где: — расход пара через последнюю ступень турбины с количеством выхлопов в конденсатор z_выхл будет равна 1.

— отношение среднего диаметра к высоте рабочих лопаток, для турбин малой мощности, который равен Θ = 7;

v_z — удельный объём пара на выходе из последней ступени;

h_вс — потери энергии с выходной скоростью, принимаемые для конденсационных турбин равен 20 кДж/кг.

В цилиндрах высокого, а иногда и среднего давления, часто принимают постоянным корневой диаметр d_к . Это позволяет обеспечить унификацию хвостовых креплений лопаток, постоянство диаметров обточки дисков, а также размеров канавок в дисках, протачиваемых для крепления лопаток. Эти ступени имеют приблизительно одинаковые профили, u/с_ф , ρ, что удешевляет их изготовление. В этом случае диаметр ступени равен d₁ = d_к + l₁ , а последней d_z = d_к + l_z . Высота лопаток последней ступени определим по формуле:

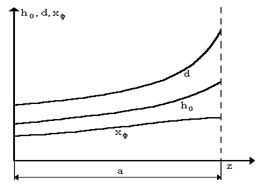
Размеры первой и последней ступеней характеризует степень раскрытия проточной части турбины, то есть изменение её диаметров. Нужно стремиться обеспечить плавность изменения диаметров вдоль проточной части, что особенно трудно выполнить при проектировании ЦНД конденсационных турбин. Определение числа ступеней турбины и разбивку теплоперепадов по ступеням производят графоаналитическим методом. В ЧНД это отношение увеличиваем от ступени к ступени, достигая в последних ступенях х_ф = 0,7.

Рисунок 5 — Диаграмма для определения числа ступеней

Располагаемый теплоперепад ступени по параметрам торможения определяем по формуле

(32)

кДж/кг

. (33)

кДж/кг

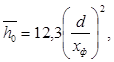
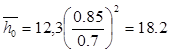
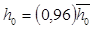
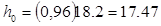
Далее отрезок а разбивают на 8 равных участков и в каждом из них определяют теплоперепад. Находим средний теплоперепад и число ступеней:

, (34)

кДж/кг

, (35)

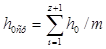
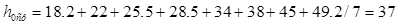
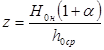
где: m – число участков. равно 7;

Н_0н – располагаемый теплоперепад нерегулируемых ступеней;

α – коэффициент возврата тепла, определяемый из соотношения.

(36)

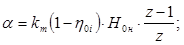
k_т = 4,8·10 -4 – коэффициент, учитывающий состояние пара.

Полученное число ступеней z округляем до целого числа, делят отрезок а диаграммы на число ступеней и определяем теплоперепады каждой ступени. Сумма теплоперепадов должна быть равна величине 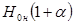. Это равенство в курсовом проекте соблюдается. Полученные теплоперепады наносим на процесс расширения в i-s-диаграмме (графический рисунок -1).

1.4 Полный расчет ступеней турбины

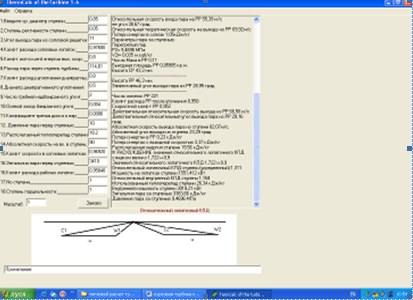
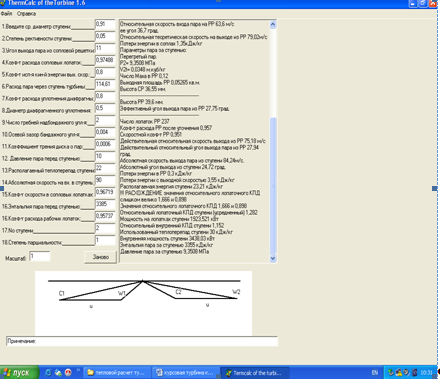
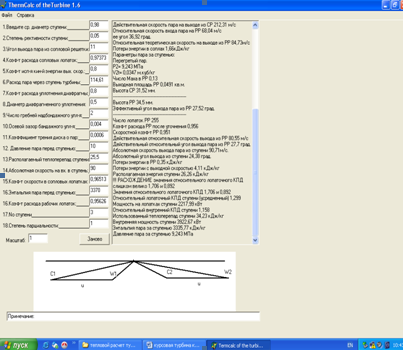
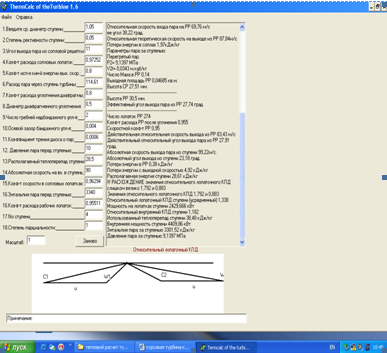
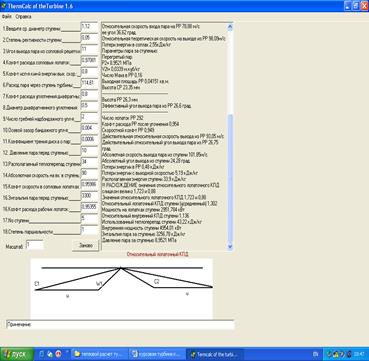
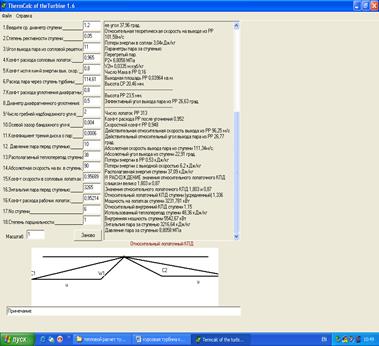
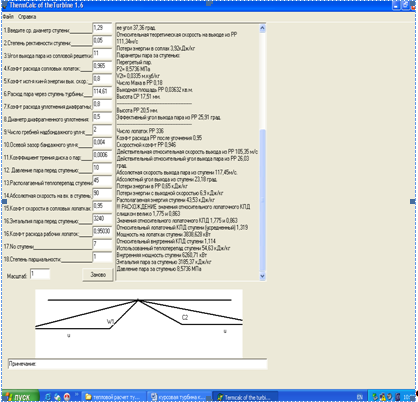
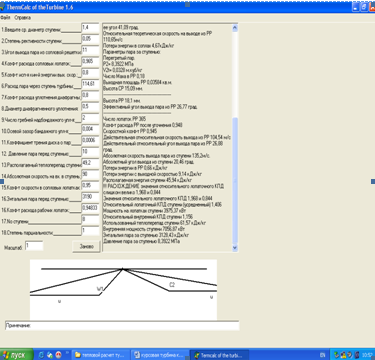
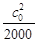
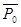
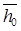
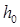
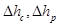
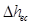
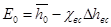
Детальный расчет промежуточных ступеней необходимо выполнять на ЭВМ, программе TermCalc of the Turbine 1.6. И рассчитаем эти параметры: расход пара D, параметры пара перед ступенью: давление Р₀ , МПа; температура (сухость) t₀ (x₀ ), энтальпия i₀ , кинетическая энергия на входе в ступень , давление торможения перед ступенью , располагаемый теплоперепад от параметров торможения , располагаемый теплоперепад от статических параметров , средний диаметр d₁ , d₂ , окружная скорость u₁ , u₂ , отношение скоростей u/с_ф , средняя степень реактивности ρ, располагаемый теплоперепад в решетке h_0с , h_0р , параметры пара за решетками, числа Маха М_{1 t} , M_{2 t} , коэффициент расхода μ₁ , μ₂ , площадь решетки F₁ , F₂ , 10 -4 м2 , эффективный угол выхода α_1Э , β_2Э , высота решетки l₁ , l₂ , 10 -3 м, относительная высота решетки l₁ /b₁ , l₂ /b₂ , относительный диаметр d₂ /l₂ , коэффициент скорости φ, ψ, скорость выхода потока из решетки с₁ , w₂ , м/с, относительная скорость на входе в рабочую решетку и абсолютная скорость на выходе из нее w₁ , с₂ , углы направления скоростей β₁ , α₂ , потери энергии в решетке , потери энергии с выходной скоростью , располагаемая энергия ступени , относительный лопаточный КПД η_ол , использованный теплоперепад h i , внутренняя мощность N_i ,энтальпия пара за отсеком i_{2 z} , кДж/кг.

Далее приведены результаты расчета ступеней:

Рисунок 1- Детальный расчет 1-ой ступени ЦНД

Рисунок 2- Детальный расчет 2-ой ступени ЦНД

Рисунок 3- Детальный расчет 3-ой ступени ЦНД

Рисунок 4- Детальный расчет 4-ой ступени ЦНД

Рисунок 5- Детальный расчет 5-ой ступени ЦНД

Рисунок 6- Детальный расчет 6-ой ступени ЦНД

Рисунок 7- Детальный расчет 7-ой ступени ЦНД

Рисунок 8- Детальный расчет 8-ой ступени ЦНД

В заключении, курсовой проект по дисциплине «Паровые и газовые турбины» по теме: «Тепловой расчет паровой турбины» успешно завершен.

Порядок выполнения курсового проекта, построение рабочего процесса турбины Р-40-130/31 и определение расхода пара на турбину, выбор и расчёт регулирующей ступени, предварительный расчёт нерегулируемых ступеней, полный расчет ступеней турбины с использованием программы TermCalc of the Turbine 1.6. Курсовой проект выполнен в следующей последовательности: выбрана принципиальная тепловая схема турбинной установки, построен в i-s-диаграмме приближённый процесс расширения пара в турбине, произведен расчёт расхода пара на турбину, выбраны тип регулирующей ступени и произвести её расчёт при оптимальном отношении u/с, выполнен предварительный расчёт первой и последней нерегулируемых ступеней заданной части турбины.

Турбина Р-40-130/31 состоит из одной регулируемой ступени и 8 нерегулируемых ступеней ЦНД. Проведен полный тепловой расчет регулируемых и не регулируемых ступеней.

Список использованной литературы

1. Методическое указание к курсовому проекту. «По дисциплинеПаровые и газовые турбины». — Астана, 2010.-26 с.

2. Щегляев А.В. Паровые турбины. – М.: Энергия, 1976. – 357 с.

3.Трухний А.Д. Стационарные паровые турбины. – М.: Энергоатомиздат, 1990. – 640 с.

4. Бененсон Е.И., Иоффе Л.С. Теплофикационные паровые турбины. – М.: Энергоатомиздат, 1986. – 272 с.

5. Леонков А.М. Паровые и газовые турбины. Курсовое проектирование. – Минск: Высшая школа, 1986. – 182 с.

6. Семёнов А.С., Шевченко А.М. Тепловой расчёт паровой турбины. – Киев: Высшая школа, 1975. – 208 с.

7.Абрамов В.И., Филиппов Г.А., Фролов В.В. Тепловой расчёт турбин. – М.:Машиностроение, 1974. – 184 с.

8. Паровые и газовые турбины. Сборник задач. Учебное пособие для вузов. Под ред. Трояновского Б.М., Самойловича Г.С. – М.: Энергоатомиздат, 1987. – 240 с.

Источник