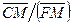Расчет числа ступеней экстракции

Расчет ступенчатых экстракторов

К этой группе экстракционных аппаратов относятся в основном смесительно-отстойные экстракторы (см. рис. 18-15), которые широко используются в химической технологии.

Однократная (одноступенчатая) экстракция (см. рис. 18-15,а). В периодически действующих экстракторах этого типа обычно процессы перемешивания и разделения фаз проводят в одном и том же аппарате. В аппарат загружают исходный раствор F концент­рацией х_н и к нему добавляют необходимое количество раство­рителя S. После интенсивного перемешивания фазы отстаивают и разделяют на экстракт Е и рафинат R.

Целью расчета такого экстрагирования является определение необходимого количества экстрагента, количества и концентрации экстракта у_к и рафината х_к.

Вначале рассмотрим случай, когда фазы практически взаимо-нерастворимы. Этот процесс может быть представлен на фазовой

диаграмме у — х (рис. 18-23). Материальный баланс такого процес­са по распределяемому веществу имеет вид

При сравнительно невысоких концентрациях распределяемого

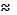
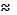
вещества Е S = G, a R F = L.

Тогда уравнение (18.16) запишется так:

Последнее выражение является уравнением прямой линии, имеющей наклон, arctg α которого равен -L/G. В качестве за­данных величин при расчете однократной периодической экстрак­ции являются количество исходного раствора F (в кг), его кон­центрация (х_н), начальная концентрация (у_н) экстрагента.

При этом расход экстрагента (в кг)

зависит от конечных концентраций у_к х_к, которые при условии достижения равновесия взаимозависимы (точка b на рис.18-23). Поэтому выбор значений G и х_к (или у_к) должен сопровождаться анализом зависимости этих величин друг от друга и стоимости проведения процесса. Отметим, что предельное насыщение экстрак­та наступает при у_{к max}. Чем больше расход эксграгента S, тем меньше arctg α, и содержание распределяемого компонента в экстракте и рафинате снижается (точка b₁ на рис. 18-23).

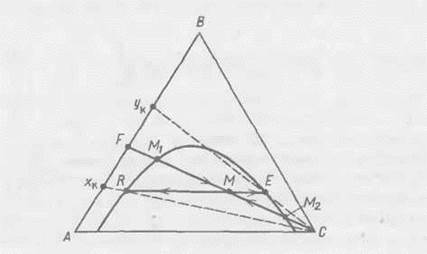
Рис. 18-24. Построение процесса однократной экстракции на треугольной диаграмме

Если же нельзя пренебречь взаимной растворимостью компо­нентов системы, то анализ и расчет процесса проводят с помощью треугольной

диаграммы (рис.18-24), которая построена по ана­логии с рис. 18-8. В этом случае соотношение между количествами исходного раствора и растворителя описывается выражением (18.5):

F/S=

причем 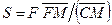, а между рафинатом и экстрактом-

выражением 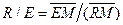(18.19)

Последнее выражение можно видоизменить следующим об­разом:

(18.20)

(18.20,а)

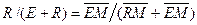
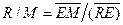
откуда можно определить количество рафината

(18.20,б)

(18.21)

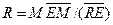
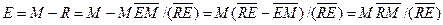
По уравнениям (18.18)-(18.21) находят количества растворителя, экстракта и рафината.

Состав рафината и экстракта можно найти, проведя из точки С лучи через точки R и E до пересечения со стороной АВ треу­гольника. Полученные точки х_к и y_к характеризуют конечные концентрации распределяемого компонента в рафинаде и экстракте соответственно.

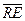
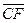
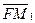
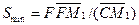
Минимальное и максимальное количество экстрагента для дан­ного процесса можно определить следующим образом. Так как точка М зависит от положения линий и , то при мини­мальном отрезке (точка М₁ находится на бинодальной кривой) будет минимальным и расход растворителя S_min:

(18.22)

При этом концентрация распределяемого компонента в рафинате будет максимальной. При перемещении по лучу CF точки М вправо до предельного — равновесного — положения (точка М₂ на бинодальной кривой) получим возможность определить макси­мальное количество растворителя S_max для данного процесса:

(18.23)

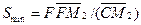
Отношение количества (расхода) экстрагента к количеству

(расходу) исходной смеси S/F называют удельным расходом экстра­гента (аналог удельного расхода абсорбента). Переписав уравнения (18.22)

и (18.23) соответственно

(18 23а) и (18.23а)

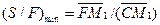
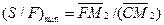
получаем выражения для определения минимального и максималь­ного удельных расходов экстрагента для данного процесса экстрак­ции. С помощью уравнений (18.22а) и (18.23а) можно проводить анализ и расчет экстракционных процессов.

Отметим, что эти уравнения можно использовать и для непре­рывной однократной экстракции; при этом величины F, S, Е, R следует относить к единице времени (например, в кг/с и т. д.).

Многократная экстракция с перекрестным движением раствори­теля. Этот вид экстрагирования отличается от предыдущего тем, что параллельно на каждую ступень (см.рис. 18-10) подают свежий растворитель в

количестве S₁, S₂ и т.д. (в кг/с). По аналогии со схемой одноступенчатого экстрагирования проведем анализ про­цесса на диаграмме у — х.

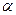
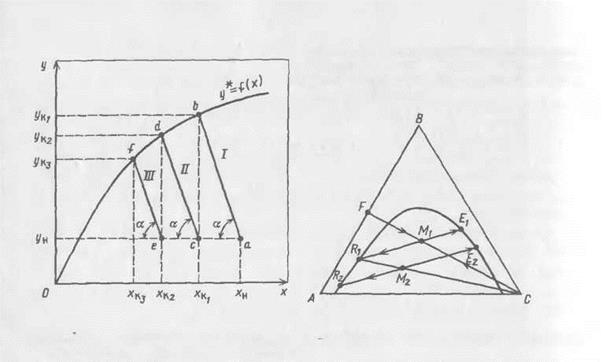Построим рабочую линию для ступени I (рис. 18-25) при условии достижения равновесия в каждой ступени. Из точки а проводим линию под углом до пересечения с кривой равновесия у* =f (х). Полученный рафинат с концентрацией х_н2 = х_к2 поступает в ступень

Рис. 18-25.Построение на диаграмме у- х процесса многократной экстракции с перекрестным движением растворителя

Рис. 18-26. К определению на треугольной диаграмме числа ступеней многоступен­чатой экстракции с перекрестным движе­нием растворителя

II. При соблюдении равенства отношения L/G в каждой ступени наклон рабочих линий будет одинаков и равен а. Поскольку концентрация свежего растворителя постоянна, то находим точку с, из которой проводим линию до пересечения с кривой равновесия (точка d), затем аналогично строим рабочую линию для ступени III и т.д. до тех пор, пока достигнем заданной концентрации х_к. Определив число ступеней, можно перейти к расчету других параметров по аналогии с расчетом однократной экстракции.

В случае частичной взаимной растворимости компонентов процесс многократного экстрагирования с перекрестным током растворителя может быть представлен на треугольной диаграмме (рис. 18-26). Линия CF описывает смешение исходного раствора и экстрагента. Затем тройная смесь состава М₁ расслаивается и разделяется на экстракт Е₁ и рафинат R₁ ступени I. Далее рафинат R₁ подвергается экстрагированию свежей порцией экстрагента S, что на рис. 18-25 отражено линией CR₁. Образовавшаяся тройная смесь М₂ расслаивается и разделяется на экстракт Е₂ и рафинат R₁ ступени II и т.д. до тех пор, пока будет получен заданный состав рафината.

Многоступенчатая экстракция с противоточным движением раст­ворителя. Вначале рассмотрим этот процесс при условии взаимной нерастворимости экстрагента и растворителя исходного раствора. В этом случае потоки чистых растворителей на ступенях не из­меняются, т.е. при движении по схеме, изображенной на рис. 18-11, потоки этих растворителей остаются постоянными.

Тогда материальный баланс по распределяемому веществу для каждой (например, i-й) ступени имеет вид, аналогичный уравнению

(18.24)

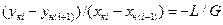
Рис. 18-27. К определению на диаграмме у — х числа ступеней многоступенчатой экстракции с противоточным

На диаграмме у — х процесс строится следующим образом

(рис.18-27). Наносится линия равновесия у* =f(x), затем для каждой ступени строится рабочая линия. Из точки а, которая находится как точка пересечения горизонтали (с ординатой у_к) с линией равно­весия, под углом наклона a

(arctg a= — L/G) проводят линию до пересечения с вертикалью х_н1 . Полученная линия аb является рабочей линией ступени I. Из точки с параллельно линии ab проводят линию до пересечения с вертикалью х_к1= х_н2 и т.д. до заданных концентраций в рафинате и экстракте. Таким образом определяют необходимое число ступеней.

Если пренебречь взаимной растворимостью компонентов нель­зя. то для анализа и расчета процесса используют треугольную диаграмму (рис. l8-28). Материальный баланс для всей установки (см. рис. 18-11)

Обозначим разность потоков в ступени I F — Е_х = Р. Тогда уравнение (18.25) примет вид

Материальные балансы каждой ступени аналогичны. Так,

При этом точки F, Р и Е₁ по правилу рычага должны лежать на

одной прямой. На одной прямой должны лежать также точки R₁, Р,Е₂и т.д.

Таким образом, если разность количеств двух любых смесей есть величина постоянная, равная Р, то прямые, соединяю­щие точки, характеризующие составы этих смесей на треугольной

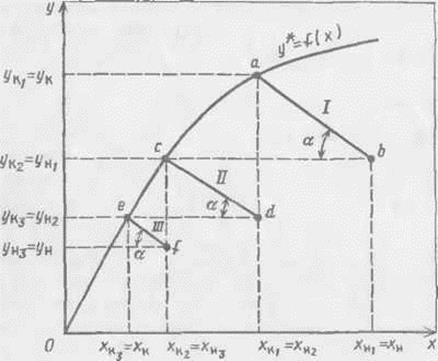
Рис. 18-28. К определению на треугольной диаграмме числа ступеней многоступенча­той экстракции с противоточным движением растворителя

диаграмме, пересекутся в одной точке Р, которую называют полюсом.

Для определения числа теоретических ступеней соединяют точки Е₁ и F, S и R_n прямыми, которые пересекаются в точке Р. Соединяя прямыми

получают коноды E_lR₁, Е₂R₂. E_nR_n, каж­дая из которых характеризует теоретическую ступень. Очевидно, что количество хорд (конод) E₁R₁, E₂R₂ и т.д. соответствует числу теоретических ступеней, необходимых для проведения данного процесса экстракции. Напомним, что при условии достижения равновесия в ступени число реальных ступеней соответствует числ> теоретических ступеней.

Отметим, что количество рафината заданною состапа зависш от удельного расхода экстрагента S/F. Больший выход рафината будет при меньших расходах экстрагента, но при этом увеличивается число теоретических ступеней. Обычно расход экстрагента принимают промежуточным между его максимальным и минимальным расходами с учетом

Источник

Расчет числа ступеней экстракции

Для аппаратурного оформления процесса экстракции нужно определить число теоретических ступеней или контактов, необ­ходимых для получения вещества заданной концентрации (чи­стоты). Существует два метода расчета числа теоретических ступеней: графический и аналитический.

Графический метод

Для графического определения необходимо иметь данные по распределению вещества между водной и органической фа­зами, заданные значения исходных и конечных концентраций в фазах и отношение потоков.

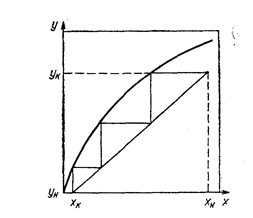
Из данных по распределению строят изотерму экстракции (или кривую равновесия) y = f(x), изображающую зависимость равновесной концентрации извлекаемого вещества в органиче­ской фазе у от концентрации в водной фазе х (рис. 58). Наклон этой кривой характеризует коэффициент распределения. В иде­альном случае до состояния насыщения равновесная линия дол­жна представлять собой прямую, так как коэффициент распре­деления постоянен; однако в реальных системах вследствие непостоянства коэффициента распределения изотерма может считаться прямолинейной только на небольшом участке.

Рис. 58. Расчет числа теоре­тических ступеней по изотерме экстракции.

Далее строится рабочая линия, выражающая связь между концентрациями в водной и органической фазах в экстракционном аппарате на основе материального баланса. Если исходная концентрация металла в органической фазе у_н, а конечная у_к; исходная концентрация в водной фазе х_н, а конечная х_к, объем водной фазы V_водн, а органической Vо_рг, то в колонну входит вещество в количестве V_воднх_н + V_оргу_н, а выходит из колонны V_воднх_к + V_оргу_к. Эти количества должны быть равны:

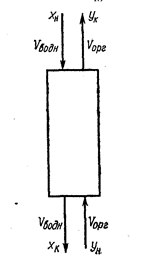
Это уравнение прямой, проходящей через точки с координатами (х_н, у_к) и (х_к, у_н). Обычно у_н = 0, х_н известно, х_к задается. Наклон прямой равен отношению V_орг/V_водн. Для любого сечения (рис. 59)

Прямая, соединяющая точки с координатами (х_н, у_к) и (х_к, у_н), наносится на график (см. рис. 58). Она называется рабочей линией. Число контактов рассчитывается графически, как пока­зано на рисунке.

Рис. 59. Схема направле­ния потоков в любом се­чении экстракционной колонны.

Аналитический метод

Аналитический метод определения числа теоретических ступе­ней применяют в том случае, если коэффициент распределения можно .принять постоянным. Тогда число теоретических ступеней рассчитывают из уравнения

где j — непроэкстрагированная часть вещества; Е’ — коэффи­циент экстракции, равный D_aV_орг/V_водн; D_a — коэффициент распределения; n — число теоретических ступеней.

Для большинства экстракционных систем этот расчет приб­лизительный, так как и коэффициенты распределения, и в неко­торой степени потоки в процессе экстракции меняются. Если эти изменения значительны, то целесообразнее расчет проводить графически.

Обычно для получения экстракта очень высокой степени чис­тоты его промывают водным раствором соответствующего соста­ва, в котором растворяется часть примесей из экстракта. Если в экстракционной системе n ступеней экстракции и т ступеней промывки, то величина j выражается уравнением

j = [(E’₁ – 1) . (E’₂ m – 1)] / [(E’₁ n+1 – 1) . (E’₂ – 1) . (E’₂ m-1 – 1) + (E’₂ m-1 – 1) . (E’₁ – 1)] (66)

Во всех расчетах определяли число теоретических ступеней, т. е. таких ступеней, на каждой из которых достигается равно­весие и фазы полностью разделяются. Но соблюдение этих ус­ловий возможно лишь на идеальной экстракционной ступени; возникает вопрос — как перейти от числа теоретических ступе­ней к числу реальных ступеней. В реальном экстракционном ап­парате в одной его секции равновесие полностью не достигается. В принципе можно построить аппарат, в секциях которого прак­тически полностью достигается равновесие и обеспечивается полное разделение фаз. Однако при этом пришлось бы значи­тельно увеличить продолжительность контакта и расслаивания. Экономичнее увеличить число реальных ступеней, допуская некоторое снижение эффективности каждой из них, но зато существенно выигрывая в их объеме.

Общая эффективность (к. п. д.) экстракционного аппарата, или средняя эффективность ступени, выражается отношением числа идеальных ступеней к числу реальных ступеней эк­стракции:

к. п. д. = n_теор / n_реальн . 100%

n_реальн = n_теор / к. п. д. . 100%

Эффективность ступени современных смесителей-отстойников обычно не менее 70-80%. Она зависит от конструкции аппара­та, определяющей тип осуществления контакта между фазами (размер капель, продолжительность контакта, скорость дви­жения жидкости и т. д.), и коэффициента диффузии экстраги­руемого компонента.

ЭКСТРАКЦИОННОЕ ОБОРУДОВАНИЕ

Для проведения процесса экстракции предложено множест­во конструкций аппаратов, однако только некоторые из них используют в промышленности.

Промышленные экстракционные аппараты обычно основаны на схеме противотока. Их можно разделить на две большие группы: экстракторы дифференциально-контактного типа с непрерывным изменением состава фаз и экстракторы ступен­чатого типа с дискретным контактом фаз, в котором на каждой ступени происходит смешение, а затем разделение фаз.

Источник