ЗАКОНОМЕРНОСТИ В СТРОЕНИИ ДРЕВОСТОЕВ
Перечислительная таксация. Подерёвный, сплошной и частичный перечёты. Разделение по толщине и категориям. Перечётная ведомость. Закономерности распределения деревьев элемента леса по толщине в однородных древостоях. Положение среднего дерева. Ранги деревьев. Редукционные числа, естественные ступени толщины.[1] с.264-295, [2] с.90-96, [4] с.50-101.
Лекция 7. .
В любом древостое, состоящем из достаточно большого числа деревьев (не менее 150. 200), можно проследить определенные закономерности в его строении: в распределении числа деревьев по их толщине, высоте, запасу и другим таксационным показателям; в характере соотношений и связей между ними. Эти закономерности наиболее четко проявляются в простейших по форме, чистых по составу, одновозрастных и не тронутых рубками нормальных насаждениях или в древостоях одного элемента леса.
Из числа выявленных закономерностей в строении насаждений отметим следующие: распределение числа деревьев, объемов отдельных стволов, сумм площадей сечений и запасов по ступеням толщины; изменение высоты, видовых чисел и видовой высоты по ступеням толщины; взаимосвязь между отдельными таксационными показателями.
Ряд распределения числа деревьев по толщине является основным показателем, определяющим строение древостоя. Он характеризует степень участия каждой ступени толщины в образовании древостоя. Все основные таксационные показатели (средний диаметр, средняя высота и др.) зависят от него. Поясним это на примере.
Допустим, что в результате перечета было установлено следующее распределение деревьев элемента леса по ступеням толщины (табл. 1).
| Ступени толщины, см | Итого | |||||||||
| Всего число деревьев, шт. | ||||||||||
| Число деревьев, % | 1,6 | 4,6 | 10,4 | 19,4 | 22,0 | 20,4 | 11,8 | 6,2 | 2,8 | 0,8 |
Если нанести данные этой перечетной ведомости на график, отложив по горизонтали ступени толщины, а по вертикали — число деревьев (рис. ), то можно заметить, что полученная кривая поднимается от тонких ступеней к средним, достигает максимума, а затем вновь снижается. Эта общая закономерность свидетельствует о том, что наибольшее число деревьев приходится на средние ступени толщины, а меньшее — на крайние (самые толстые и самые тонкие).
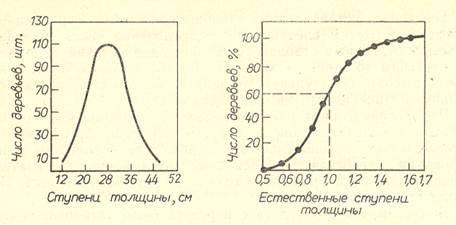
В нормальных насаждениях, состоящих из одного элемента леса, распределение деревьев по ступеням толщины характеризуется симметричной одновершинной кривой, называемой кривой нормального распределения.Для насаждений сложных, смешанных, разновозрастных или пройденных рубками, вид кривой меняется. Например, для сложных разновозрастных древостоев, состоящих из нескольких пород и поколений, кривая может иметь две вершины или больше; в молодняках или насаждениях, пройденных рубками ухода по низовому методу, вершина кривой смещается вправо, в сторону толстых ступеней, а в древостое, пройденном выборочными рубками, влево, т. е. наблюдается асимметричное распределение, и т. д.
Исследованием строения насаждений занимались многие зарубежные и отечественные ученые. Еще в 1880 г. немецкий ученый В. Вейзе выявил, что среднее по толщине дерево древостоя занимает строго определенное место. Оказалось, что число деревьев тоньше среднего диаметра составляет 57,5% от общего их числа, а толще 42,5%. Австрийский лесовод А. Шиффель (1903), изучая распределение числа деревьев и их таксационных показателей в процентном ряду от самого тонкого, до самого толстого установил, что в чистых, простых по форме древостоях независимо от абсолютной величины их среднего диаметра определенному рангу дерева, т. е. положению в про- центном ряду, соответствуют определенные редукционные числа(отношение абсолютных значений таксационных показателей деревьев любого диаметра к их средним значениям). Зная редукционные числа и средние значения таксационных показателей древостоя, можно найти значения этих показателей для любого дерева, занимающего разное положение в древостое без данных натурных измерений. Допустим, в еловом древостое со средним диаметром 40см требуется найти диаметр дерева, отстоящего от самого тонкого на 30 %.
Тогда d30=Dср*Rd=40*0,84=33,6 см, где Rd — редукционное число по Шиффелю, равное 0,84.
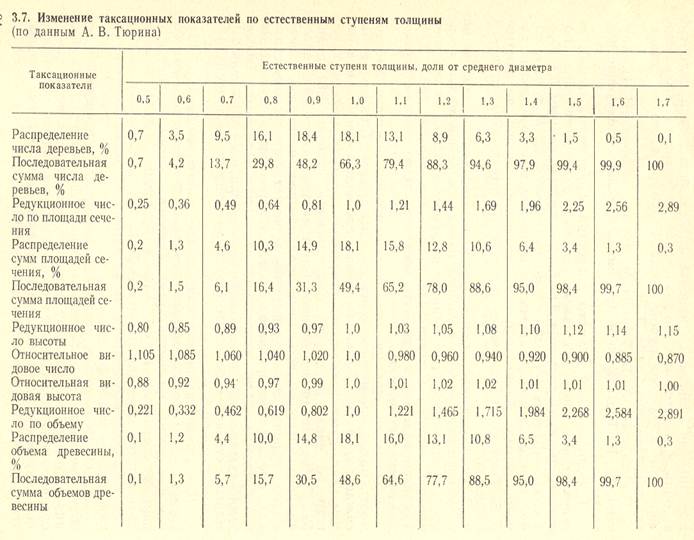
Из отечественных ученых наибольший вклад в изучение закономерностей строения насаждений внесли А. В. Тюрин и Н. В. Третьяков. Чтобы привести различные ряды распределения к сопоставимому виду, А. В. Тюрин перешел от абсолютных ступеней толщины в сантиметрах к относительным, выраженным в десятых долях от среднего диаметра, т. е. к редукционным числам по диаметру Rd. Относительные ступени толщины, являющиеся общими для всех насаждений и не зависящие от конкретных метров, А. В. Тюрин назвал естественными ступенями толщины.Принимая значение таксационного при знака среднего дерева насаждения за единицу, он проследил изменения по естественным ступеням не только диаметров, но и других таксационных признаков древостоев и выявил, что процентное распределение деревьев по естественным ступеням толщины не зависит от породы, класса бонитета и полноты, а лишь в некоторой степени зависит от возраста и большей мере от характера рубок ухода.
По данным А. В. Тюрина и других авторов (Н. П. Анучина, Н. В. Третьякова и др.) можно сделать следующие выводы:
1. Если средний диаметр древостоя Dср принять за 1,0, то редукционное число Rd самых тонких его деревьев равно половине среднего диаметра 0,5 Dcр (по другим данным 0,4 Dср), а самых толстых — 1,7 Dср (в молодняках 2. 2,5 Dср), т. е. самое толстое дерево в древостое примерно в 4 раза толще самого тонкого. Таким образом, все число стволов, по данным А. В. Тюрина, укладывается в рамки 13 естественных ступеней толщины.
2. Если последовательно суммировать число стволов по естественным ступеням толщины, начиная с самой малой (тонкой), и по полученным данным построить график, то получим кривую, которая в статистике называется огивой (рис. 2). Такие же графики могут быть построены и по суммам площадей сечений и запасам.
Располагая такими графиками, можно показать зависимость между диаметром деревьев и их местом (рангом) в насаждении по числу стволов, сумме площадей сечений и запасам. Так, суммарное число стволов в ступенях меньше среднего по диаметру дерева (естественная ступень 1,0) равно 57. 58%, или, иначе, среднее (по диаметру) дерево находится на 58-м месте по проценту числа стволов, начиная с самой малой ступени.
Эта закономерность может быть использована для определения среднего диаметра нормальных насажденийнепосредственно по перечетной ведомости. Для этого достаточно суммировать проценты числа стволов по направлению от малых ступеней к большим (толстым), пока не наберется 58% (округленно 60 % ).
Для ряда распределения, приведенного выше (табл.1.), средний диаметр оказывается принадлежащим к ступени 28, так как сумма процентов числа деревьев от ступени 12 до ступени 28 составляет 1,6+4,6+10,4+19,4+22,0=58%. К ступени 28 относятся деревья диаметром 26,1. 30 см. Поскольку в расчет попадают все деревья этой ступени, средний диаметр насаждения равен 30 см,
3. Дерево, имеющее средний диаметр, имеет и среднюю высоту, среднюю площадь сечения, средний объем и т. д., или, иначе, среднее по диаметру дерево в древостое является также средним и по остальным таксационным показателям. Эта связь используется для определения средних таксационных показателей древостоя (метод средней модели).
4. Редукционные числа по площади сечения и по объему так же, как их ряды распределения и огивы, очень близки. Так, самые тонкие деревья древостоя по площади сечения составляют 0,25, а по объему 0,22 от среднего дерева, а самые толстые по обоим показателям 2,89. Это значит, что объем тонкого дерева составляет всего 22% от объема среднего дерева, а объем самого толстого больше среднего в 2,9 раза. Площадь сечения и объем самого тонкого дерева в насаждении в 12 раз меньше, чем самого толстого. Максимальный процент (18,1%) как по сумме площадей сечений, так и по объему приходится на среднюю ступень толщины. Доля участия крайних ступеней очень мала 0,1. 0,3 %, Близость редукционных чисел по площади сечения и объему свидетельствует о том, что между ними имеется очень тесная прямолинейная зависимость, она характеризуется коэффициентами корреляции 0,92. 0,98.
5. Между диаметром и высотой по естественным ступеням толщины наблюдаются определенные соотношения. Если среднюю высоту насаждения принять за 1,0, то пределы высоты будут: минимальный 0,80, максимальный 1,15; в молодых насаждениях эти пределы несколько больше, а в старых меньше. Связь высоты с диаметром довольно тесная и характеризуется высоким корреляционным отношением, равным 0,95 и выше.
6. Относительный сбег и полнодревесность стволов, характеризуемые коэффициентами формы и видовыми числами, уменьшаются от низших ступеней толщины к высшим. Изменение видовых чисел по естественным ступеням толщины выражается линейным уравнением.
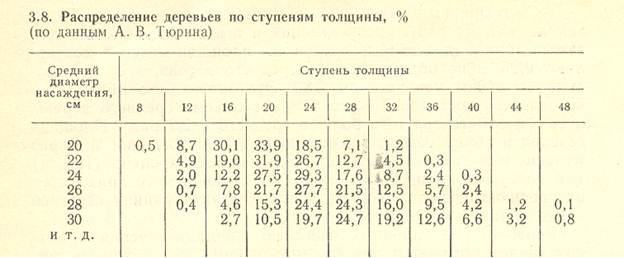
Изложенные основные закономерности строения насаждений имеют большое теоретическое и практическое значение. В частности, А. В. Тюрин на основании полученных им данных составил специальные таблицы распределения числа деревьев для насаждений с различными средними диаметрами (табл. 3.8).
Аналогичные таблицы составлены по суммам площадей сечений и запасам. По ним, не имея данных перечета, а зная лишь средний диаметр древостоя, можно распределить общий запас по отдельным ступеням толщины. Подобные таблицы служат также основой для составления товарных таблиц, в которых приведено распределение запаса по сортиментам.
Н. В. Третьяков установил, что закономерности строения древостоя, установленные для нормальных насаждений, свойственны каждому элементу леса смешанных и сложных насаждений. Приведенные выше закономерности позволяют судить о границах изменения и средних значениях отдельных таксационных показателей всего насаждения и его отдельных частей. Они облегчают изучение леса и служат основой для разработки более рациональных методов его учета. Однако при изучении закономерностей строения насаждений надо иметь в виду, что они носят статистический характер и выявляются только в насаждениях с достаточным числом деревьев. Возводить эти закономерности в абсолютный закон не следует. Попытка произвести подобные расчеты на ограниченном материале может привести к значительным отклонениям от приведенных рядов распределения.
Источник
Задание 2. Оценка распределения деревьев в насаждении по толщине
Развитие лесных насаждений протекает на основе известных законов диалектики: единства и борьбы противоположностей, перехода количества в качество, отрицания отрицания. Согласно принципам этих законов, все явления в лесу органически взаимосвязаны, причинно обусловлены, находятся в постоянном движении и изменении.
Определенные статистические закономерности обнаруживаются также в строении древостоев. В таксации леса под строением древостоев понимается совокупное сочетание варьирования таксационных показателей, распределения деревьев по их значениям и взаимосвязей последних между собой в определенных возрастах леса.
Строение древостоя в момент наблюдений отражает его состояние как функции возрастной динамики совокупности совместно произрастающих древесных растений определенной исходной структуры в однородных лесорастительных условиях [20]. Под строением понимают определенный порядок сочетания деревьев, который может быть охарактеризован их составом, взаимным расположением и связями между ними.
В результате взаимодействия деревьев между собой в процессе роста и развития, влияния окружающей среды и реакции организмов на эти влияния, таксационные показатели деревьев в древостое оказываются чрезвычайно изменчивыми и в то же время закономерно взаимосвязанными между собой.
На строение древостоев влияют природные факторы (лесорастительные условия, происхождение, полнота, породный состав, возрастное строение и др.) и антропогенные.
Закономерности в строении древостоев имеют важнейшее значение в теории и практике лесоучетных работ. Выявленные закономерности в строении древостоев позволяют повысить производительность лесов путем правильного хозяйственного вмешательства в жизнь леса, создать оптимальную структуру лесов будущего, достигаемую лесокультурными приемами и рубками ухода в молодых возрастах в естественных насаждениях.
Также они позволяют определять запас древостоев, вычислять выход сортиментов, служат основой составления различных лесотаксационных таблиц и нормативов учета леса. Использование закономерностей морфологических показателей леса приобретает важное значение при разработке автоматизированных методов дешифрирования аэрофотоснимков и применении других способов дистанционного изучения лесов.
Из всех таксационных показателей в курсовой работе рассматривается только строение древостоя основного элемента леса по толщине, т.е. по диаметрам деревьев. Распределение числа деревьев по ступеням толщины дает общее представление о строении насаждения [1].
Наиболее наглядно его можно изучить графически. При этом по оси абсцисс откладывают ступени толщины, а по оси ординат количество деревьев в соответствующих ступенях толщины. Соединение полученного ряда точек дает кривые распределения деревьев по толщине.
Данные для построения графика на рис. 4.4 журнала берут из перечетных ведомостей ПП для основной породы, предварительно пересчитанные по формуле (44) на 1 га. Пример графика распределения деревьев по толщине приведен на рис.8 пособия.
Рис. 8. Распределение деревьев по толщине, шт/га
При построении такого графика для простых, чистых, одновозрастных насаждений получают одновершинное распределение.
В одновозрастных чистых насаждениях, созданных путем посева и посадки и имевших до смыкания крон деревьев одинаковый уход, распределение деревьев по толщине характеризуется симметричной одновершинной линией, описываемой кривой нормального распределения.
Часто после смыкания крон вследствие конкуренции между деревьями у кривых распределения по толщине появляется асимметрия. Более крупные деревья, занимающие в насаждении лучшее положение, имеют все преимущества для успешного роста, и поэтому характеризующая их правая ветвь кривой распределения становится длиннее. При этом левая ветвь отстающих в росте деревьев становится более короткой за счет отпада ослабленных деревьев.
Также асимметрия наблюдается в молодняках или в результате вырубки отстающих деревьев при рубках ухода. В спелых и перестойных насаждениях асимметрия может быть следствием проведения в них выборочных рубок с целью вырубки наиболее крупных деревьев.
С увеличением возраста насаждения характер распределения деревьев изменяется в зависимости от древесной породы и хода изреживания. В результате конкуренции между деревьями они разделяются на классы роста и развития и затем образуют главный и подчиненный полог. В этом случае в кривой распределения деревьев по толщине образуется двухвершинность. Вырубка при уходе за лесом или при выборочной рубке деревьев средних размеров также ведут к двухвершинности в распределении.
С учетом всего вышеперечисленного студент должен сформулировать вывод под рис. 4.4 журнала по данным своих ПП.
Для построения графика на рис. 4.5 журнала сначала необходимо рассчитать процентное соотношение количества деревьев по ступеням толщины для всех ПП. При этом общее кол-во деревьев на пробе принимается равным 100%. График распределения деревьев по толщине в относительных величинах представлен на рис. 9 пособия.
Рис. 9. Распределение деревьев по толщине, %
По данному графику легко заметить, что все вершины кривых ПП стали примерно равны, т.е. находятся в диапазоне от 15 до 30%. Также заметнее стала видна асимметрия и двухвершинность некоторых кривых. Студенты должны сделать вывод под рис. 4.5 журнала и объяснить имеющиеся на графике особенности.
Источник