Пример расчет монолитных лестниц

Расчет монолитной железобетонной лестницы в Лире. Пример расчета. Видео.

Сегодня я хочу с вами поделиться алгоритмом расчета монолитной лестницы в программном комплексе Лира 9.6. В конце статьи вас ждет видео, но сначала немного теории и пояснений.

Имеется у нас лестница, один ее марш с площадками изображен на рисунке, а рассчитывать мы будем один этаж лестницы с двумя маршами.

Ступени (выделено красным) мы учитываем как нагрузку. Работе конструкции они не помогают, а лишь нагружают лестничный марш. А вот элементы, включенные в расчет, — это лестничные площадки и марши (выделено синим).

Итак, давайте начнем расчет.

Видеоурок вы найдете внизу статьи ↓

Сбор нагрузки.

1. Нагрузка от собственного веса марша и площадки определится автоматически.

2. Нагрузка от веса ступеней.

Нагрузка от веса ступени вертикальная, она не перпендикулярна маршу. Мы ее будем задавать в виде неравномерно распределенной нагрузки на каждую ступень (подробнее в видео). Изменяется она от нуля до максимального значения, равного высоте ступени 0,15 м, умноженной на вес железобетона 2,5 т/м³ и на коэффициент надежности по нагрузке 1,1:

0,15∙2,5∙1,1 = 0,41 т/м².

Выглядеть в итоге эта нагрузка будет так:

3. Временная нагрузка от веса людей 0,3 т/м² (согласно ДБН «Нагрузки и воздействия) с коэффициентом 1,2:

4. Нагрузка для проверки на зыбкость (согласно ДСТУ Б В.1.2-3:2006 «Прогибы и перемещения») – 0,1 т.

Построение расчетной схемы.

Расчетная схема лестницы состоит из трех площадок и двух маршей между ними. Результаты расчета для площадки можно смотреть только по средней площадке, так как к нижней и верхней приложена нагрузка лишь от одного марша.

Опирание площадок в данной задаче – по одной стороне. Вместе с маршем площадки образуют устойчивую конструкцию, по сути ломаная по высоте плита, опирающаяся по двум сторонам. С таким же успехом можно смоделировать и площадки, опирающиеся по трем сторонам, и даже марши, заведенные наружным краем на стену – нужно просто зафиксировать нужные узлы.

Важный нюанс в построении схемы: количество элементов вдоль марша должно быть равно количеству ступеней, так проще будет задавать нагрузку от собственного веса ступеней.

Задание жесткости.

Толщина и площадок, и марша одинакова. Жесткости в расчете мы задаем две: одну с обычным значением модуля упругости бетона, вторую – с пониженным (для расчета по второму предельному состоянию). Сначала мы назначим пониженный модуль упругости, сделаем расчет и проверим перемещения, а затем вернемся в исходные данные, сменим модуль упругости на обычное для железобетона значение и пересчитаем, чтобы уже посмотреть эпюры усилий и выполнить расчет арматуры.

Задание нагрузки.

Три загружения соответствуют трем типам нагрузки:

1. Собственный вес и вес ступеней – постоянная нагрузка с коэффициентом надежности по нагрузке 1,1. Кстати, для расчета по второму предельному состоянию коэффициент равен 1,0, это в расчете не учтено, а желательно бы поиграться. Но у нас и с повышающими коэффициентами все прошло с запасом.

Нагрузка от веса ступеней выглядит так:

На каждой ступеньке она меняется от нуля до максимального значения.

Вместе с собственным весом получается так:

2. Временная нагрузка.

3. Нагрузка для проверки на зыбкость – сто кило в середине марша.

Для проверки нагружаем только один марш, так как марши одинаковые.

Напоминаю. Проверка на зыбкость диктует следующее условие: при нагружении лестничного марша в центре пролета нагрузкой 100 кг марш должен прогнуться (вертикальное перемещение) менее, чем на 0,7 мм.

Почему важна проверка на зыбкость? Если конструкция не проходит по расчету граничное условие, лестница будет играть под ногами. Это не будет угрожать целостности конструкции (до определенных пор), но дискомфорта людям принесет немало. Просто страшно ходит по лестнице, которая трясется от каждого шага.

Кстати, после задания всех нагрузок нужно бы сгенерировать таблицу РСУ (расчетные сочетания усилий), о чем я благополучно забыла во время записи видеоурока. Прощаю себе потому, что рассматриваю результаты (усилия и армирование) по РСН (расчетному сочетанию нагрузок). Но лучше об РСУ не забывать, особенно в более сложных расчетах.

Выполнение расчета для проверки деформаций лестницы.

После того, как была построена расчетная схема, заданы связи, нагрузки, жесткости, можно запускать задачу на расчет и смотреть результаты.

В результатах в первую очередь генерируем РСН (расчетное сочетание нагрузок). У нас три загружения, из них два первых сочетаются между собой. Мы, конечно, можем посмотреть результаты по каждому загружению и просуммировать их, но зачем, если программа позволяет нам воспользоваться ее возможностями? Поэтому генерируем РСН (расчет на зыбкость в сочетания не включаем, он идет отдельным сочетанием) и ищем наихудший результат.

В деформациях нам интересны только перемещения по оси Z, вот их и проверяем. У нас деформация лестничного марша максимум 8 мм. При пролете 5400 мм. Согласно ДСТУ «Прогибы и перемещения» максимальный прогиб не должен превышать L/200. Проверим:

5400/200 = 27 мм > 8 мм.

Условие выполняется, наш прогиб меньше максимально допустимого.

Также нужно проверить условие расчета на зыбкость. Прогиб от нагрузки размером в 0,1 т, приложенной в центре пролета, составляет 0,05 мм – значительно меньше 0,7 мм, значит все в порядке.

Выполнение расчета для определения усилий в лестнице.

Раз с перемещениями все в пределах нормы, можно вернуться в исходные данные, заменить жесткость на обычную (Е=3е006) и пересчитать задачу.

В результате расчета мы получаем результаты, готовые для экспорта в ЛирАРМ. Посмотрим на эпюры моментов и поперечных сил – они не вызывают вопросов и выглядят вполне логично. Кстати, если бы местные оси пластин не совпадали с глобальными осями (я об этом говорю при построении расчетной схемы), с эпюрами усилий была бы путаница – все было бы не то и не так. Этот вопрос я вынесла в отдельную статью (там же есть наглядное видео), можете изучить (статья в разработке).

Переход в ЛирАРМ и расчет армирования лестницы.

Последний этап – расчет армирования лестницы. Здесь никаких особенностей нет. Импортируем в ЛирАРМ, задаем материалы, выполняем расчет по РСН или РСУ (последнее нужно было сформировать в предыдущем окне) и читаем результаты.

Нижняя рабочая арматура:

Верхняя рабочая арматура:

Все готово для конструирования. Им мы тоже займемся в одной из следующих статей.

Спасибо вам за внимание, а вот и видеоурок.

Вопросы по расчету можно задать в комментариях.

Источник

Расчёт монолитного жетезобетонного марша.

Расчёт монолитного жетезобетонного марша.

Характеристики:

· Марш шириной 1,5 м.

· Высота этажа 2,25 м.

· Угол наклона марша α = 30⁰

· Размер ступеней 15 х 30 см.

· Бетон класса В20

· Согласно табл. П4 И П6: R_b = 11,5 Мпа; R_bt = 0,9 Мпа; E_b = 24 ٠ 10 3 МПа)

· Арматура каркасов класса А-IV (согласно табл. П12 R_s = 610 МПа,

Определение нагрузок и усилий.

g n = 0,2٠1,5٠1٠25٠0,95٠1,1= 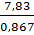= 9 кН/м.

Расчётная схема приведена на рис.1.46, а.

-Временная нормативная нагрузка:

-Коэффициент надёжности по нагрузке γ_ϯ = 1,2.

-Длительно действующая временная нагрузка = 1 кН/м 2 .

· Расчётная нагрузка на 1 м длины марша:

g = ( g n ٠ γ_ϯ + p n ٠ γ_ϯ ) = ( 9٠1.1 + 3٠1.2 )٠1.5 = 20.25 кН/м.

· Расчётный изгибающий момент в середине пролёта марша:

М = = = 26.27 кН٠м.

· Поперечная сила на опоре:

Q = 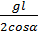= = 35 кН.

Предварительное назначение размеров сечения марша.

— Назначаем толщину плиты = 30 мм, высоту рёбер (косоуров) h = 170 мм, толщину рёбер b_r = 80 мм. (рис 1.46, б). Действительно сечение марша заменяем на расчётное тавровое с полкой в сжатой зоне ( рис. 1.46, в): b = 2b_r = 2٠80 = 160 мм; ширину полки при отсутствии поперечных рёбер принимаем не более = 2 (l/6) + b = 2 (300/6) + 16 = 116 см или = 12 + b = 12٠3 + 16 = 52 см.

Подбор площади сечения продольной арматуры.

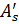
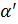
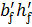
— По условию M ≤ R_bb_x (h₀ – 0.5_x) + R_sc (h₀ — ) устанавливаем расчётный случай для таврового сечения (при x = ): при M ≤ R_bγ_b2 (h₀ – 0.5 ) нейтральная ось проходит в полке: 2 627 000 ≤ 11,5٠(100)٠0,9٠52٠4.2٠(14,5 – 0,5٠3) = 2 938 572 Н٠см; условие удовлетворяется, нейтральная ось проходит в полке; расчёт арматуры выполняем по формулам для прямоугольных сечений шириной = 52 см.

A₀ = 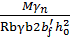= = 0.220.

По табл. П10 находим ƞ = 0,875; ξ = 0,6;

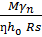
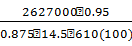
A_s = = = 3.22 см 2 .

По табл. П9 принимаем 3 d = 12 A-IV с A_s = 3.39 см 2 . В каждом ребре устанавливаем по одному плоскому каркасу К-1 (рис. 1.47).

Расчёт наклонного сечения на поперечную силу

— Поперечная сила на опоре 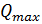= 35٠0,95 = 33.2 кН. Вычисляем проекцию расчётного наклонного сечения на продольную ось c по формуле

Рис. 1.47. Армирование лестничного марша

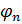
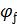
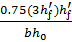
где: = 0; =2 = 2 = 0.220 2 = 4.2 ٠ 10 5 Н/см.

В расчётном наклонном сечении Q_b = Q_sw = Q/2, а так как по формуле:

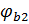
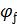
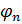
Q_b = [ (1+ + )R_btb ]/c,

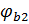
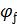
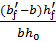
где c – длина проекции наиболее опасного наклонного сечения на продольную ось элемента; – коэффициент, принимаемый в зависимости от вида бетона

= 0,75 ,

но не более 0,5; Q_b = B_b/2, то с = B_b/0.5Q = 4.2٠10 5 /0.5٠19000 = 44.2 см больше 2h₀ = 29 см. Тогда Q_b = B_b/c = 4.2٠10 5 /29 = 14.6٠10 3 H = 14.6 кН.

— Дополнительно в ¼ пролёта назначаем из конструктивных соображений поперечные стержни диаметром 8 мм из стали класса A-I с шагом s = 80 мм ( не более h/2 = 170/2 = 85 мм), A_sw = 0.503 см 2 ; R_sw = 175 МПа; для двух каркасов n = 2, A_sw = 1.060 см 2 ; μ_w = 1.060/16٠8 = 0.0083; α = E_s/E_b = 1.9٠10 5 /2.4٠10 4 = 7.91. В средней части рёбер поперечную арматуру располагаем конструктивно с шагом 200 мм.

— Проверяем прочность элемента по наклонной полосе между наклонными трещинами по формуле:

Q ≤ 0,3 ,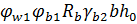

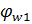
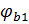
= 1 + 5α μ_w = 1 + 5٠7,91٠0,0083 = 1,33

= 1-0.01٠14.5٠0.9 = 0.87.

Q = 33.2 2 = 34 618 МПа ٠см 3 = 34,61 кН٠м

Расчётная схема плиты.

Для средних пролётов плиты:

М = ± q /16

Для крайних пролётов:

М = ± q /11

где l – расстояние в свету между гранями балок; l_к – расстояние от грани балки до середины опоры плиты на стене (при ширине опоры около 120 мм)

Сбор нагрузки на балку.

Расчётная нагрузка на 1м балки при ширине грузовой площади = 5,8 м

От веса пола и железобетонной плиты g₁ = 8.11٠5.8 = 47 кН

От веса выступающего ребра балки g₂ (h — )b =(0.4 – 0.06)٠0.2٠25٠11=1.9 кН

Временная: ⱴ = 9.6٠5.8 = 55.7 кН

Всего: g = 104.7 кН

Статический расчёт балки.

Для крайних пролётов при глубине заделки балок в стены на 25 см

= — /2 – 0.25/2 = 4 – 0.15 -0.125 = 3.725 м

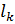
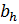
M = q /11 = 104.7 ٠3.725 2 /11 = 132 кН٠м

— М = — q /14 = — 104,7٠3,725 2 /2 = — 103,8 кН٠м

Q_a = q /2 + (-M) / = 104.7٠3.725/2 – 103.8/3.725 = 167.1 кН

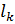
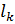
Q_b = 195 + 27.9 = 223 кН

Для средних пролётов и средних опор:

М = ± q /16 = ± 104,7٠ /16 = 89,6 кН٠м

Q = 0.5 q = 0.5٠104.7٠5.7 = 193.7 кН

Для средних пролётов балки определяют минимальные изгибающие моменты от неблагоприятного расположения временной нагрузки ⱴ = 55,7 кН/м

На смежных пролётах при отношении ⱴ/g = 1,13

В сечении 6 на расстоянии от опоры 0,2l = 0.2٠3.7 = 0.74 м.

М₆ = — 0,33٠104,7٠3,7 2 = -47,3 кН٠м

в сечении 7 на расстоянии от опоры 0,4l = 0,4٠3,7 = — 1,48 м

М₇ = -0,012٠104,7٠3,7 2 = -17,2 кН٠м

Расчёт монолитного жетезобетонного марша.

Характеристики:

· Марш шириной 1,5 м.

· Высота этажа 2,25 м.

· Угол наклона марша α = 30⁰

· Размер ступеней 15 х 30 см.

· Бетон класса В20

· Согласно табл. П4 И П6: R_b = 11,5 Мпа; R_bt = 0,9 Мпа; E_b = 24 ٠ 10 3 МПа)

· Арматура каркасов класса А-IV (согласно табл. П12 R_s = 610 МПа,

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Источник