Построение падающей тени от ограждения на лестницу



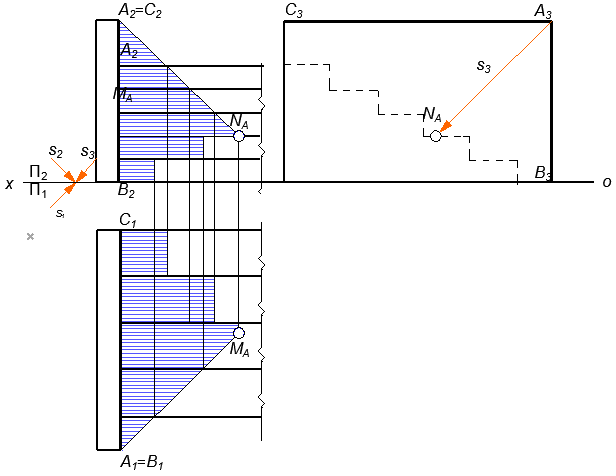
Рассмотрим рисунок 21. Для построения тени от ограждения на лестницу обязательно нужна 3-я проекция. Тень бросает плоскость САВ, ограниченная прямыми АВ и АС. Луч S3 определяет положение тени от точки А на лестницу (NA).
Прямая АВ параллельна подступенкам (вертикальный элемент) и перпендикулярна проступям (горизонтальный элемент) лестницы. Поэтому тени от нее на подступенки параллельны самой прямой, а на проступях совпадает с фронтальной проекцией луча S1.
Прямая АС параллельна проступям лестницы и перпендикулярна подступенкам. Тени от нее на проступи параллельны самой прямой, а на подступенки совпадает с горизонтальной проекцией луча S2 .
Рисунок 21- Тень от ограждения на лестницу
Литература
1 Брилинг Н.С., Балягин С.Н. Черчение. справ. пособие – М.: Стройиздат, 1994.;417с. ил;
2 Крылов Н.Н. Начертательная геометрия. [Текст] – М.; Высшая школа; — 2005;. 224 с ил.
Источник
Падающая тень от лестницы
Собственные и падающие тени на фасадах зданий
Представление о внешнем виде здания в основном создается по чертежу фасада. Поэтому рассмотрим примеры построения теней от различных элементов фасада, используя те же приемы, что и при построении теней геометрических тел (см. раздел 12.6).
Рассмотрим сначала примеры построения теней некоторых частей здания.
На рис.12.25а в аксонометрии (построение теней в аксонометрии см. главу 11.6), а на рис.12.25б в прямоугольных проекциях показано построение падающих теней от козырька (или балкончика) здания. Для построения теней в аксонометрии использована вторичная проекция козырька. Пример. Построить точку пересечения К вертикальной прямой i с плоскостью Б (АВС). Т.к. вырожденный вид прямой имеет ся на виде сверху, то решение начинаем с него.
Тени в нишах. Ниши это углубление в стене. Если задняя грань ниши параллельна фронтальной плоскости проекций, ниши называют плоскими
Тень, падающая от фронтального обрамления ниши, повторит его форму на задней грани.
На рис. 12.26а в аксонометрии, а рис. 12.26б на ортогональном чертеже дано построение проекций собственной и падающей теней прямоугольной ниши. Изучив чертеж, можно установить, что строить нужно проекции лишь падающей тени от ребер АВ и ВС. От вертикального ребра АВ (проекции А1В1, А2В2)тень падает на горизонтальную плоскость П1 и на фронтальную плоскость задней стенки ниши (рис. 12.26б). Как известно, тень, падающая от вертикальной прямой на горизонтальную плоскость, совпадает с горизонтальной проекцией светового луча, а тень, падающая от вертикальной прямой на фронтальную плоскость, параллельна этой прямой (см. раздел 12.3).
От горизонтальной прямой ВС (В1С1, В2С2) тень падает частично на заднюю фронтальную стенку ниши в виде прямой, параллельной ребру ВС, и частично на правую боковую грань ниши (на чертеже не изображена), где она параллельна профильной проекции луча света, так как ребро ВС занимает профильно – проецирующее положение.
На рис. 12.27а показано построение тени в нише, перекрытой полуциркульной аркой.
Для построения тени в нише необходимо построить тень от прямой АВ и от дуги окружности, проходящей через точки В и С. Тень от дуги окружности будет окружность того же с центром в точке От. На рис. 12.27б построения выполнены в системе прямоугольных проекций.
На рис. 12.28а показано построение тени аналогичное построению теней в прямоугольной нише. Здесь тени от отрезков АВ, ВС, СД параллельны самим отрезкам.
В цилиндрической нише (рис.12.28 б) падающая тень ограничена прямой линией, делящей нишу пополам, и четвертью окружности.
Падающие тени от выступающих частей здания. Рассмотрим как строятся падающие тени от нависающих карнизов зданий.
Тень от карниза на рис. 12.29 падает от прямых АВ, ВС и СД. Тень от прямой АВ будет параллельна самой прямой, так как прямая параллельна той плоскости, на которую падает тень. Тень от прямой ВС ложится на фронтальную плоскость параллельно самой прямой, а тень от прямой СД, как от прямой, перпендикулярной фронтальной плоскости, пройдет по направлению светового луча. Ребро выступа Е дает тень, параллельную самому себе на фронтальной плоскости проекций.
На рис. 12.30а показано построение тени от полуколонны на стене и от абака (прямоугольной плиты) на колонну и на стену, а также собственная тень колонны. Полуколонна имеет форму полуцилиндра. Построение падающей тени от колонны и абака на стену основано на том, что линии, от которых падает тень, занимают частное положение. Через тень точки С на стене проходит три линии, поэтому строятся три тени. Тень от СД вертикальна, тень от АС горизонтальна, тень от прямой, проходящей через точку С перпендикулярно к стене, параллельна фронтальной проекции луча света. Тень от последней прямой расположена внутри тени от абака. Через точку Д также проходят три линии. Тень от одной из них (СД) построена, тень от горизонтальной прямой, параллельной стене, не нужна, так как она находится внутри тени от абака, тень от прямой, перпендикулярной стене, параллельна фронтальной проекции световых лучей. Тень падающая от колонны найдена по собственной тени колонны, как показано на рисунке. Эта тень будет вертикальна, так как вертикальна граница собственной тени.
Через точку А проходит три линии. Тень от вертикальной прямой не нужна, так как эта прямая не принадлежит границе собственной тени абака. Тень от прямой АС – в натуре дуга эллипса – проецируется на плоскость П2 в дугу окружности. Тень от АВ параллельна фронтальной проекции светового луча.
Если абак полуцилиндр (рис. 12.30 б), то нужно взять на нижнем основании цилиндра некоторое количество точек и, проведя через них лучи света, определить тени точек на поверхности колонны. Точка С пересечения границы собственной тени колонны с границей тени, падающей от абака на колонну, построена методом обратных лучей (см. раздел 12.5) (через точку С2т* проведен обратный луч до пересечения с границей собственной тени в точке С2т). Так же с помощью обратного луча построена точка А*, в которой граница падающей тени пересекается с левой контурной образующей колонны; вначале построена точка А1, затем найдена точка А2. Через точку А2 проведена фронтальная проекция луча света, которая пересекается с фронтальной проекцией образующей в точке А2*.Граница тени, падающей от абака на стену, представляет собой две дуги эллипсов и отрезок прямой, касательной к ним.
Тень на лестнице. На рис. 12.31 и 12.32 дан фрагмент лестницы и входа в здание в виде прямоугольной ниши. На рис 12.31 показано построение в аксонометрии, а на рис. 12.32 в прямоугольных проекциях собственных и падающих теней элементов крыльца. Тень на земле от вертикальной прямой АВ параллельна горизонтальной проекции светового луча. Строится точка 1 пересечения этой тени с вертикальной гранью первой ступени и проводится тень на этой грани параллельно АВ. Через точку 2 проходит тень от прямой АВ параллельно тени той же прямой на земле. Проведя луч света через точку А строим тень Ат от этой точки на горизонтальной грани первой ступени. Тень от прямой АС на первой ступени Ат3 параллельна самой прямой АС.
Тень от прямой АС на вертикальную грань второй ступени и плоскость стены проходит параллельно фронтальной проекции светового луча. Построение тени от боковой части лестницы на земле и стене ясно из чертежа.
Аналогичная задача в ортогональных проекциях показана на рис. 12.32. горизонтальная проекция тени от прямой АВ на плоскости земли и на горизонтальной грани первой ступени по направлению совпадают с горизонтальной проекцией луча света. Тень от прямой АС на горизонтальные плоскости ступеней параллельна горизонтальной проекции самой прямой АС. Тень на плоскость стены и вертикальную грань второй ступени совпадает по направлению с фронтальной проекцией светового луча.
Тени на крышах зданий. Скат крыши это наклонная плоскость. Трубы, антенны, смотровые окна и т.д. отбрасывают тень на плоскость ската. На рис. 12.33 показано построение тени от трубы на скат крыши и от одного ската на другой.
При построении этих теней используется метод секущих плоскостей (см. раздел 12.2). Проведем через ребро трубы 1-2 горизонтально проецирующую плоскость Р параллельно горизонтальной проекции светового луча и найдем линию пересечения АВ пересечения этой плоскости со скатом крыши. Точку 12т получим, проведя фронтальную проекцию светового луча до пересечения с фронтальной проекцией прямой АВ. Тени точек 3 и 5 найдены аналогично. При построении тени от одного ската на другой проводим через точку С горизонтально проецирующую плоскость R и находим линию пересечения 6-7 этой плоскости со скатом крыши. На фронтальной проекции определяем тень точки С2т и тут же отмечаем точку Д тени на коньке. Контур тени замыкается точкой Е, так как она лежит на скате крыши. Тень на противоположном скате крыши определяется по произвольной точке К.
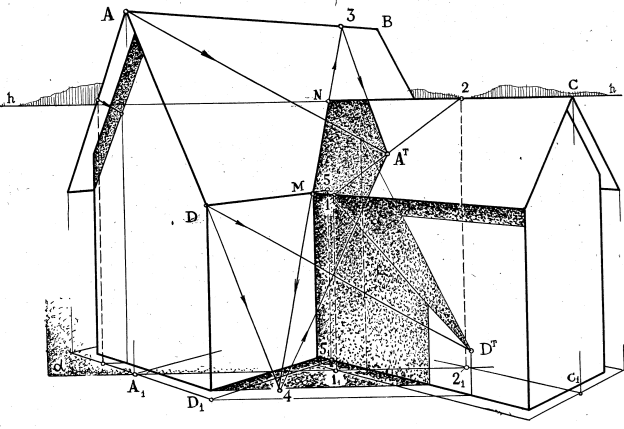
На рис.12.34 приведен пример построения теней на фасаде и плане здания. Собственные тени элементов здания на чертеже не видимы, кроме тени на крыше, которая будет видимой на горизонтальной проекции. Начинают построения с определения падающей на горизонтальную плоскость проекций тени здания, используя для этого характерные точки здания: углы карниза, конек карниза. Затем строят тени от трубы на скат крыши и от одного ската на другой, используя при этом метод секущих плоскостей (см. раздел 12.2) и метод обратного луча (см. раздел (12.5). Построение ведется в следующей последовательности:
1. Строим тени точек 4, 5, 6, 7 и 8 на горизонтальную плоскость проекций П1;
2. Соединяем тени точек 4 – 5 и 6 –7 – 8;
3. Т. к. свесы 1-4, 6-9, 8-10 и конек крыши 2-5 прямые, параллельные плоскости проекций П1, то их тени на эту плоскость будут параллельны самим прямым (см. раздел 12.3);
4. Тени от углов В и С будут совпадать с горизонтальной проекцией световых лучей (см. раздел 12.3);
5. Тень от трубы на плоскость П1 строится аналогично по точкам 11 и 12;
6. Точки пересечения теней от свеса 8 –10 и конька 5 – 2, а также от свеса трубы 12 – 13 и свеса крыши 7 – 8 методом обратного луча (см раздел 12.5) возвращаем на скат крыши;
7. Тень от трубы на скат крыши и от более высокого ската строиться методом секущих плоскостей (см. раздел 12.2) так, как было описано в рис. 12.33;
8. Тень свеса 1 – 2 на передней плоскости здания на фронтальной проекции будет параллельна самому свесу, т.к. 1 – 2 // П2;
9. Тени от выступа стены и свеса крыши 3 – 9 на стену получены:
а) от вертикального отрезка Д тень Д2Т будет параллельна самому отрезку;
б) от горизонтальной прямой 3 – 9 тень на плоскость будет совпадать с направлением светового луча и проходить через точку 32Т;
в) от свеса 2 – 3 тень будет проходить через точку 32Т и /параллельно самому свесу, т.к. прямая 2 – 3 //П2;
г) точку пересечения теней FТ методом обратного луча возвращаем на свес 6 -9 и соединяем точкой 22Т.
10.Тень от свеса 6 – 9 на плоскость стены будет проходить параллельно самому свесу.
Источник
Глава 3 тени в перспективе
Проекционные чертежи, выполняемые в процессе проектирования, помимо удобноизмеримости и метрической определенности, должны быть наглядными и должны давать возможно более полное представление о композиции и внешнем облике здания, о его пластическом решении в деталях. Достичь этого можно с помощью построения теней. Построение тени на ортогональном чертеже, в аксонометрии и перспективе состоит из следующих этапов:
1) выполнение контуров (границ) теней точными приемами геометрических построений;
2) выявление и передача на чертеже градаций освещенности с учетом физических закономерностей.
Ниже рассматриваются примеры построения теней в перспективе, применительно к зданиям и их фрагментам, а также основные графические изобразительные приемы. Эти примеры помогут студентам при выполнении задания по теме «Перспектива здания».
Тени обогащают изображение, делают его еще более выразительным и убедительным, а с применением графических изобразительных приемов придают максимальную наглядность перспективе. Свободное рисование теней не имеет проекционной связи с элементами здания и не дает возможности выявления и устранения ошибок в пропорциях будущего сооружения.
3.1 Построение теней в перспективе
Для придания перспективным изображениям большей выразительности строят собственные и падающие тени изображенных объектов. В основу этих построений положены геометрические предпосылки теории теней, рассмотренные ранее при изучении начертательной геометрии. Не повторяя их заново, перейдем к конкретным примерам построения, на которых покажем некоторые особенности, присущие этим методам.
Построение теней в перспективе имеет много общего с аналогичными построениями в аксонометрии. Так же как и в аксонометрии, в перспективе для построения теней необходимо задать направление светового луча и иметь на чертеже его вторичную проекцию. Но поскольку в основе перспективы — центральное проецирование, а не параллельное, то и лучевые прямые, их проекции, параллельные в пространстве, имеют в перспективе свои точки схода.
Так как источник света S считается удаленным в бесконечность, то вторичная проекция его должна быть на линии горизонта. В зависимости от направления лучей и положения источника света относительно зрителя и картины возможны следующие три основные схемы теней (рис. 3.1).
На первой из них солнце находится позади зрителя, слева. При этом точка схода проекции лучей расположена на горизонте S1, точка схода самих лучей (перспектива солнца S) — ниже горизонта на одной вертикали с точкой S1.
На второй схеме солнце расположено перед зрителем. Теперь перспектива солнца (S) находится впереди зрителя выше горизонта на одной вертикали с точкой S1.
На третьей схеме лучи света параллельны картинной плоскости, поэтому они изображаются и на перспективе параллельными, а вторичные их проекции — параллельными основанию картины, т.е. горизонтальными.
Очевидные удобства построений по третьей схеме позволяют использовать ее для выполнения задания. Все дальнейшие примеры будут даны по этой схеме.
3.2 Основные приемы построения
Лучи света, падая на поверхность какого-либо тела, образуют на ней освещенную и неосвещенную часть (рис. 3.2). Тень, образующаяся на неосвещенной части предмета, называется собственной тенью.
Линия, разделяющая на поверхности предмета освещенную и затененную части, называется контуром собственной тени (линия АОВ). В свою очередь, данный предмет отбрасывает тень на тела, находящиеся позади него. Тень, образующаяся от одного предмета на другом, называется падающей тенью, а ее внешняя граница — контуром падающей тени (линия АО Т В).
Рассматривая рис. 3.2, мы видим, что между контуром собственной и падающей тени существует прямая связь: оба контура образуются лучевой поверхностью, как бы обертывающей данный предмет и пересекающей затем предметную плоскость.
Иными словами, контур падающей тени является тенью контура собственной тени.
Таким образом, нашей задачей является построение контуров теней. Выявление градаций освещенности внутри зоны тени и света будет рассмотрено ниже.
При выполнении задания используем три основных способа построения теней:
1) способ следа луча — основан на том, что тень, падающая от точки, является следом луча, проведенного через эту точку, т.е. луч S встречается с предметной плоскостью в той точке О Т , где он пересекается со своей вторичной проекцией S1 (рис. 3.2).
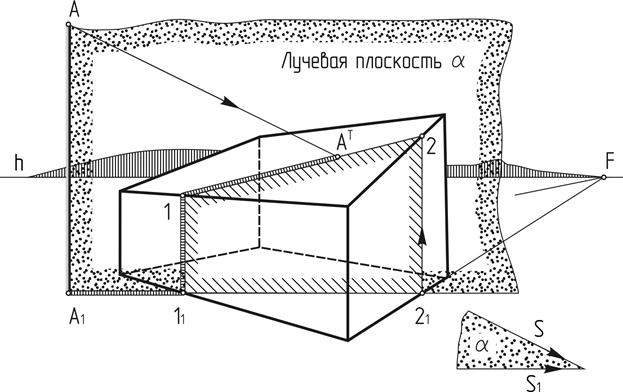
2) способ лучевых сечений — состоит в том, что при построении теней как собственных, так и падающих предметы рассекаются плоскостями, параллельными лучу света, т.е. параллельными плоскости картины. Так на рис. 3.3 лучевая плоскость a (рассекает предмет по линии 111221, на которой и будет падающая тень от прямой АА1 отрезками 111 и 1А Т . Этим способом можно построить собственные и падающие тени любых поверхностей, хотя и построения могут быть весьма насыщенными и сложными.
3) Способ обратных лучей — применяется, как правило, для построения падающих теней от одного предмета на другой. Способ заключается в определении точек пересечения контуров падающих теней от одной и другой модели на предметной плоскости. Из этих точек затем проводятся обратные лучи до пересечения с контуром собственной тени предмета, на котором строится тень от другого предмета.

Так, на рис. 3.4 падающая тень от прямой АВ состоит из трех отрезков — А1, 1-2 и 2 Т В Т . На предметной плоскости построен контур падающей тени предмета и тень прямой АВ. Точка 2 Т в пересечении контура NМ Т с тенью прямой АВ Т обратным лучом перенесена на контур собственной тени предмета, т.е. на ребро NМ. Далее построение видно из чертежа.
Способ обратных лучей очень прост и дает возможность легко строить характерные точки падающей тени — ее пересечения с контуром собственной тени.
3.3 Тень от точки и отрезка прямой на горизонтальные и вертикальные плоскости
Для получения тени от точки А (рис. 3.5) на чертеже через точку А и ее вторичную проекцию проводят соответственно луч S и его вторичную проекцию S1 до их взаимного пересечения. Полученная точка А Т — след луча на предметной плоскости, т.е. тень от точки А.
Для нахождения тени от отрезка различного положения методом следа луча учитывают следующие положения начертательной геометрии:
1) если прямая перпендикулярна горизонтальной плоскости, то ее тень на этой плоскости совпадает со вторичной проекцией светового луча или параллельна ей (рис. 3.6 и рис. 3.7);

2) если прямая параллельна какой-либо плоскости, то ее тень на этой плоскости параллельна прямой. Для вертикальных прямых их параллельность своим теням на вертикальных плоскостях сохраняется и в перспективе (рис. 3.6,б; рис. 3.7), а для горизонтальных прямых эта параллельность в пространстве учитывается в перспективе общей точкой схода F на линии горизонта (рис.3.8, рис.3.9).
На рис. 3.9 тени от вертикальных прямых АА1 и ВВ1 либо совпадают с направлением вторичной проекции светового луча S1 (отрезки А11 и В15 на предметной плоскости), либо ему параллельны на горизонтальных площадках предмета (отрезки 6-7, 8В Т и 2А Т ). На вертикальных плоскостях предмета тени от прямых АА1 и ВВ1 им параллельны (отрезки 1-2, 5-6 и 7-8).
Тени от горизонтальной прямой АВ на горизонтальных площадках предмета имеют общую точку схода F на линии горизонта (отрезки А Т 3 и 4В Т ). Отрезок тени 3-4 получен по построению:
сначала построена тень В Т , затем проведен отрезок В4 с направлением в точку F, аналогично найдена тень точки А — А Т , и проведен отрезок А Т 3 с направлением в точку F, наконец, соединены точки 3 и 4.
На рис. 3.10 показано построение тени от стержня АК (кронштейна), выходящего из плоскости вертикальной стены под прямым углом.
Тень от точки А получена на предметной плоскости методом следа луча. Отрезок тени до стены А Т 1 имеет направление в точку F т.к. кронштейн горизонтален. Тень на стене получена соединением точки перелома тени 1 с основанием К кронштейна.
На рис. 3.11 построена тень от стержня АК, выходящего из плоскости стены под произвольным углом.
Тень от точки А построена методом следа луча. Затем на стержне АК нужно взять одну произвольную точку, например, М и построить от нее тень. Соединив тень А Т с тенью М Т , которые расположены в предметной плоскости, продолжим линию А Т М Т до пересечения с основанием стены, а затем точку перегиба тени 1 соединим на плоскости стены с основанием стержня К.
Если тень от вспомогательной точки М попадет на стену (рис. 3.12), то построение тени нужно начинать, соединив основание стержня К с полученной тенью М Т вспомогательной точки М до места перегиба — основания стены и закончить построение ломаной линии тени, соединив точку перегиба 1 с тенью А Т точки А.
На основании предыдущих построений выполним перспективу падающей тени от вертикальной стенки на лестницу и тени от ступеней лестницы на предметную плоскость — поверхность земли и другие поверхности (рис. 3.13).
1. Тень от вертикального ребра ВВ1 на предметную плоскость и на горизонтальную плоскость 1 ступени параллельна вторичной проекции светового луча, т.е. параллельна основанию картины.
2. Тень от того же ребра ВВ1 на вертикальную плоскость подступенка 1 ступени параллельна самому ребру.
3. Тени от горизонтального ребра ВЕ на параллельные ему плоскости ступеней имеют общую с самим ребром точку схода F на линии горизонта.
4. Тени от ребра ВЕ на вертикальные плоскости подступенков II и III направлены к точкам С и D, в которых прямая ВЕ пересекает продолженные вверх плоскости подступенков (аналогично построению на рис. 3.10).
5. Тень от точки А построена методом следа луча, аналогично построены тени от точек М и N.
6. Контуры теней подступенков на предметной плоскости параллельны горизонтальной проекции светового луча, т.е. горизонтальны.
7. Контуры теней горизонтальных проступей, как и перспектива их ребер, идущих из точек А, М и N, имеют общую точку схода F.
8. Тени ребер ВЕ и NК на вертикальную плоскость фасада пройдут через их основания, т.е. через точки Е и К от точек перегиба 2 и 1 (аналогично рис. 3.10). Остальные построения ясны из чертежа.
Пример построения тени в перспективе .от выступающих элементов здания на плоскость стены и плоскости оконных ниш даны на рис. 3.14.
1. Тень от карниза построена с помощью вспомогательной точки М, взятой произвольно на выступе карниза, т.к. карниз параллелен плоскости стены, то его тень имеет с перспективой карниза общую точку схода на линии горизонта. Левая крайняя точка карниза К определяет дальнейшее построение его тени, что видно из чертежа.
2. Тень от оконных откосов в нише проема строится на примере точки 1 или 2. Вертикальный откос имеет свою тень также вертикальной, а горизонтальный откос и его тень имеют общую точку схода на линии горизонта.
3. Тень падающая от балконной плиты определяется контуром собственной тени этой плиты. Итак, контур собственной тени балконной плиты состоит из отрезков: NА , АВ, ВС и СD . Построена мнимая тень (А Т ) от точки А, на этой же линии в перспективе находится тень от точки В. Зная точку схода параллельных линий, можно провести контур тени (А Т )В Т от отрезка АВ на плоскость стены.
В оконных нишах эта тень смещена и построение ее показано, на чертеже.
Отрезок ВС параллелен стене здания, т.е. его тень В Т С Т расположена вертикально.
Основания отрезков АN и СD точки N и D соединить соответственно с полученными ранее тенями (А Т ) и С Т точек А и С.
4. Падающие тени от ограждения балкона построены на основании ранее приведенных примеров как тени от отрезков, параллельных и перпендикулярных плоскости стены здания.
Аналогичные построения необходимо выполнить при наличии других архитектурных и конструктивных элементов, выступающих из плоскости стены (пояски, пилястры, колонны, козырьки над входной дверью и т.д.). Задача упрощается тем, что почти все перечисленные элементы здания имеют горизонтальные и вертикальные ребра и плоскости, параллельные или перпендикулярные плоскости стены здания
3.4 Тень от точки и прямой на наклонные плоскости
Основным приемом построения падающих теней на наклонную плоскость является метод лучевых плоскостей, отмеченный ранее на рис. 3.3. Тень от вертикального стержня на наклонную плоскость крыши (рис. 3.15) построена в следующем порядке.
1. Проведена вертикальная лучевая плоскость, параллельная картине, через вертикальный отрезок и, естественно, через его вторичную проекцию. Основание этой плоскости, т.е. горизонтальный след, пересекается с основаниями вертикальных стен в точках 11 и 21. Поднимем эти точки на контур наклонной кровли (точки 1 и 2) и выделим общий контур сечения — трапецию 11221.
2. Полученное сечение, вертикальный отрезок АА К и луч S находятся в одной лучевой плоскости a. Проведя луч S через точку А до пересечения с контуром сечения, найдем в пересечении точку А Т — тень от точки А. Соединив ее с основанием мачты (точка А К ), получим падающую тень от мачты на наклонной плоскости крыши здания.
Используя описанные приемы, покажем на примере построение падающей тени от трубы на крышу (рис. 3.16).
1. Определим контур собственной тени призмы трубы. Это отрезки А К А, АВ, ВС, СС К , от которых и нужно строить контур падающей тени.
2. Проводим первую лучевую плоскость a через отрезок АА К А1 и найдем его падающую тень на крыше — точка А Т (как на рис. 3.15).
3. Аналогичное построение нужно провести, построив тень от точки В с помощью второй лучевой плоскости a2 (точка В Т ).
4. Соединив точки А Т и В Т , получим тень от отрезка АВ трубы.
5. Отрезок ВС трубы параллелен крыше, поэтому построение его тени связано с точкой В и общей точной схода F1 на линии горизонта. Прямая, идущая из точки В Т в точку схода F1 в пересечении с лучом, проведенным из точки С трубы, даст тень от этой точки — С Т .
6. Соединив С Т с основанием этого угла трубы (точкой С К ) с учетом видимости отрезка прямой, завершим построение контура падающей тени от трубы.
Аналогичные построения нужно проводить для нахождения падающих теней на наклонные плоскости крыши от других элементов, имеющих место быть на кровле здания: коробок вентиляционных каналов, слуховых окон, антенн и т.д.
3.5 Построение теней отдельных элементов здания
На рис. 3.17 построена тень от конька АВ, падающая на крышу пристройки и тень от ближайшего свеса высокой крыши на стену пристройки.
1. Тень А Т точки А строим при помощи секущей лучевой плоскости, проведенной через точку А. Горизонтальный след лучевой плоскости пересекает вторичную проекцию пристройки по точкам 11 и 21 (свес и конек). Найдем эти точки на перспективе свеса и конька пристройки — точки 1 и 2. На пересечении луча 3 из точки А с этой линией 12 и будет отмечена тень точки А — А Т .
2. Продолжим разжелобок МN до пересечения с коньком в точке 3 и соединим 3 искомой прямой с А Т .
3. Продолжим разжелобок МN до пересечения с продолжением свеса АD) в точке 4 и соединим точку 4 с точкой А Т , получим искомую тень.
4. Построим тень от точки D на стену пристройки — точка D’.
Точка D— это пересечение двух отрезков — свеса АD и карниза DМ. Отрезок АD параллелен стене пристройки, значит, его тень будет ему параллельна, а на перспективе эти две прямые будут иметь общую точку схода выше горизонта.
5. Отрезок DМ перпендикулярен стене пристройки, найдем его пересечение с этой стеной ( по вторичной проекции) и закончим построение тени свеса крыши, соединив точки .D Т и 5.
3.6 Построение теней здания
Используя приведенные примеры, ведем построение от крупных форм к мелким деталям (рис. 3.18).
Если взята низкая линия горизонта, то необходимо использовать опущенный план, так как исходный план «смятый» и его применение может привести к значительным ошибкам. Выбор угла наклона светового луча связан с конструкцией здания и главная задача при этой — дать максимально наглядное графическое изображение на плоскости чертежа всех архитектурных и конструктивных элементов.
Источник