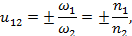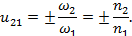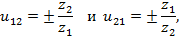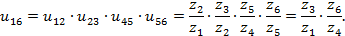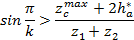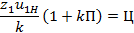Разбивка передаточного отношения по ступеням
Разбивка передаточного отношения по ступеням
- Разбивка передаточного числа При проектировании многоступенчатой передачи возникают проблемы оптимального выбора количества ступеней и распределения передаточных чисел по ступеням. Решение этой проблемы зависит от требований к передаче. Не существует унифицированного решения для конструкций, используемых для малой мощности, измерительных приборов и снижения мощности. Наиболее важным в приборостроении является минимизация размеров, массы, скорости или инерции и минимизация ошибок передачи.
Условия, которые минимизируют размеры. При равных передаточных числах расстояние между приводом и выходным валом минимально. ’12 = ’23 = … = ‘ Людмила Фирмаль
Условия минимизации массы. Оптимальное количество шагов в зависимости от условий (14,5) «Опт = 3 Джиу. (14,6) Поскольку уменьшение количества шагов повышает эффективность передачи, рекомендуется округлить значение, полученное в уравнении (14.6), до более низкого целочисленного значения. Оптимальное передаточное число для этапа составляет 2,16. Условия минимизации уменьшения момента инерции. Использование низкоинерционных передач ускоряет работу механизма в режиме пуска / останова и обеспечивает стабильность системы слежения.
Момент инерции механизма минимизируется за счет минимального веса и габаритов колеса. Низкооборотное шаговое колесо мало влияет на момент инерции. Поэтому рекомендуется уменьшить передаточное число высокоскоростной ступени. Колеса легко нагруженной скоростной ступени должны быть изготовлены из пластика. Оптимальное количество шагов определяется уравнением (14.6). Используйте номограмму, показанную на рисунке, чтобы найти приблизительное передаточное число для каждой ступени в 14.13. Передаточное число для первой ступени / 12 определяется следующим образом.
- На правой вертикальной шкале номограммы найдите раздел, соответствующий общему передаточному отношению / 1 л. Затем проведите прямую линию через этот сегмент и точку, помеченную крестиком, который соответствует общему количеству шагов. Пересечение этой прямой с левой вертикальной шкалой указывает передаточное число первой ступени / 12. Например, для f1 = 100 и lopt = 6 мы решили, что f12 = 1.5 (рисунок 14.13). Передаточное число последующей ступени in_x составляет i 1ya / / 12. Затем в правой вертикальной шкале найдите сегмент, который соответствует передаточному отношению ступени, и нарисуйте прямую линию, которая проходит через точку, соответствующую этому сегменту, и крест, обозначенный шагом -1.
Общая ошибка передачи зависит от ошибки каждой ступени. Следовательно, чем меньше количество шагов, тем меньше ошибок. Если максимально возможное передаточное число в уравнении (14.5) равно 8, iopt = 1,11 log /, „. Это значение лопасти округляется до ближайшего целого числа. Последний шаг вносит существенный вклад в общую ошибку передачи. Максимальное передаточное число равно 8. Передаточное число первой ступени равно / | 2 = i \ n / 8π’1. Рисунок 14.13 В устройстве передачи энергии разумным условием распределения ступенчатого общего передаточного числа iXn является достижение значения напряжения, близкого к минимальной массе материала зубчатой передачи для различных ступеней.
Пересечение этой прямой и левой вертикальной шкалы указывает передаточное число второй ступени. Людмила Фирмаль
При переходе от ведущего звена редуктора к выходу частота вращения уменьшается, а крутящий момент увеличивается. Чтобы уменьшить натяжение зубьев зацепления, увеличьте ширину колеса медленного шага. Передаточное число высокоскоростной ступени может увеличивать передаточное число тихоходной, чтобы приблизить массу колеса.
Если вам потребуется заказать решение по прикладной механике вы всегда можете написать мне в whatsapp.
Источник
Отношение передаточных чисел ступеней
Передаточные числа одноступенчатых передач приведены в табл. 5.5. В многоступенчатых передачах и в редукторах передаточное число следует разбить по ступеням. От разбивки общего передаточного числа по ступеням в двух- и трехступенчатых редукторах (а также в коробках передач) в значительной степени зависят удобство смазывания колес и компоновки деталей, а также конструкция корпуса и его габариты.
Универсальных рекомендаций по разбивке передаточного числа по ступеням, удовлетворяющих всем указанным условиям, не существует. Выбор способа разбивки передаточного числа зависит от конкретных требований, которым должна отвечать конструкция: обеспечения минимальных габаритов редуктора и минимальной массы зубчатых колес, получения одинакового погружения зубчатых колес всех ступеней в масляную ванну, создания наименьшей установочной площади корпуса редуктора и др. [15].
В основу решения задачи о разбивке передаточного числа иногда кладут условие полного использования нагрузочной способности всех ступеней редуктора [5]. Стандартные передаточные числа для цилиндрических одно-, двух- и трехступенчатых редукторов и их разбивка по ступеням приведены в табл. 5.6 (механические характеристики материалов всех колес примерно одинаковы). В соосных редукторах иногда 
где 
— коэффициенты ширины колес соответственно тихоходной и быстроходной ступеней.
В коническо-цилиндрических редукторах принимают такие же значения передаточных чисел, как и в цилиндрических многоступенчатых (см. табл. 5.6). В зубчато-червячных редукторах для
зубчатой пары принимают передаточное число не выше 2. 2,5 (при этом получается удобная компоновка деталей в корпусе). В червячно-зубчатых редукторах для зубчатой пары принимают передаточное число 
Для двухступенчатых червячных редукторов удобство компоновки требует обеспечения 
где 
и — межосевые расстояния тихоходной и быстроходной ступеней. При этом передаточные числа тихоходной и быстроходной ступеней получаются примерно равными 
Когда частота вращения ведомого вала должна иметь не одно, а несколько конкретных значений, применяют коробки передач, которые обеспечивают ступенчатое изменение передаточных чисел. При проектировании коробок передач часто принимают ряды частот вращения валов в виде геометрической прогрессии со знаменателями 
. Тогда частоты вращения валов будут: 
Источник
Отношение передаточных чисел ступеней
Лабораторная работа №14
Определение передаточных отношений зубчатых передач
Цель работы – изучить различные виды зубчатых передач, научиться определять тип и вид зубчатых передач, их передаточные отношения и передаточные числа.
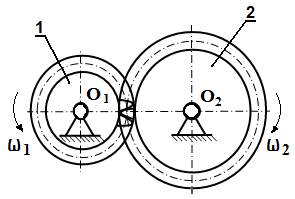
Зубчатая передача – трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару (рис.1).
Рис.1. Зубчатая передача с внешним зацеплением
Парное зубчатое колесо — зубчатое колесо передачи, рассматриваемое по отношению к другому зубчатому колесу данной передачи. Зубчатое колесо 2 (рис.1) является парным колесу 1, зубчатое колесо 1 парное колесу 2.
Шестерня – зубчатое колесо передачи с меньшим числом зубьев.
Колесо – зубчатое колесо передачи с большим числом зубьев.
Передаточное отношение зубчатой передачи – это отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого зубчатого колеса .
Ведущее зубчатое колесо – зубчатое колесо передачи, которое сообщает движение парному зубчатому колесу.
Ведомое зубчатое колесо — зубчатое колесо передачи, которому сообщает движение парное зубчатое колесо.
Передаточное отношение u 12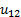 
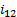
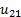
(иногда используется обозначение i 12 
) определяется при ведущем колесе 1, передаточное отношение u 21 
определяется если ведущим является колесо 2:
u 12 =± ω 1 ω 2 =± n 1 n 2 , 
u 21 =± ω 2 ω 1 =± n 2 n 1 . 
Рис.2. Виды зубчатых зацеплений: внешнее (слева) и внутреннеее
Передаточное число зубчатой передачи – это отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса. Передаточное число зубчатой передачи определяется по формуле:
u 12 =± z 2 z 1 и u 21 =± z 1 z 2 , 
где z 1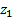 
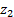
и z 2 
— числа зубьев колес 1 и 2, соответственно.
Знак «+» берется для внешнего зацепления (рис.1 и рис.2), знак «–» для внутреннего зацепления. Виды зацеплений приведены на рис.2. Знаки учитываются только для зубчатых передач с параллельными осями вращения колес.
Типы зубчатых передач
Цилиндрическая зубчатая передача (показана на рис.3, ее кинематическая схема – на рис.1) — зубчатая передача с параллельными осями, у зубчатых колес которой аксоидные, начальные и и делительные поверхности цилиндрические. В этих передачах относительное расположение осей вращения колес определяется только межосевым расстоянием.
Аксоидная поверхность зубчатого колеса – каждая из поверхностей, описываемых мгновенной осью относительного движения зубчатых колес передачи, относящаяся к данному зубчатому колесу. В цилиндрической и конической передачах начальные поверхности совпадают с аксоидными.
Коническая зубчатая передач (показана на рис.3) — зубчатая передача с пересекающимися осями, у зубчатых колес которой аксоидные, начальные и и делительные поверхности конические. В этих передачах относительное расположение осей вращения колес определяется только углом между осями.
Ортогональная зубчатая передача (показан на рис.3) – коническая зубчатая передача, угол между осями которой равен 90°.
Неортогональная зубчатая передача – коническая зубчатая передача, угол между осями которой отличен от 90°.
Рис.3. Типы зубчатых передач (слева), коническая (в центре), винтовая зубчатая передача
Зубчатая передачи со скрещивающимися осями вращения колес (рис.3) — зубчатая передача, в которой относительное расположение осей вращения колес определяется межосевым расстоянием и углом между осями. Существует много вариантов таких механизмов. На рис.3 показана винтовая зубчатая передача, угол между осями которой составляет 90 °. Другой вариант передачи с углом между осями в 90 ° — червячная передача (рис.4). Шестерня червячной передачи называется червяком (поз.1 на рис.4) , а колесо – червячным колесом (поз.2 на рис.4) . Вторая передача, показанная на рис.4, называется гиперболоидной. Аксоиды ее зубчатых колес – однополостные гипеболоиды вращения.
Для конических зубчатых передач и передач со скрещивающимися осями передаточное отношение определяется по тем же формулам, что и для цилиндрических передач, но без учета знаков.
Рис.4. Червячная (слева) и гиперболоидная зубчатая передача
Виды зубчатых колес
Рис.5. Виды зубчатых колес: цилиндрическое косозубое (слева), шевронное (в центре),
В зависимости от вида зубьев зубчатые колеса цилиндрических передач делятся на прямозубые (рис.3 слева), косозубые и шевронные (рис.5). Зубчатые колеса конических передач – на прямозубые (рис.5), тангенциальные, с круговым зубом (рис.3 в центре), с криволинейным зубом.
В зависимости от профиля зубьев зубчатые колеса и передачи делятся на эвольвентные (рис.2, рис.6), циклоидальные, зубчатые колеса цилиндрической передачи Новикова (рис.6), профили зубьев которой контактируют по дуге окружности.
Рис.6. Виды зубчатых колес: с эвольвентным профилем зубьев (слева),
зубчатые колеса передачи Новикова
МНОГОСТУПЕНЧАТЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
Зубчатые передачи с неподвижными осями вращения колес
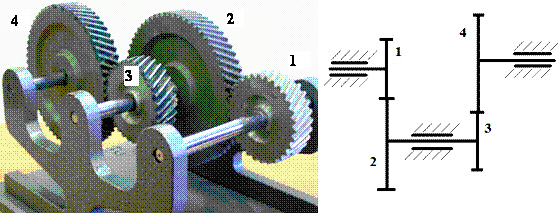
Рис.7. Двухступенчатая зубчатая передача и ее кинематическая схема
Простейший зубчатый механизм (рис.1) состоит из двух зубчатых колес ведущего и ведомого, которые одновременно являются входным и выходным, соответственно. Для получения необходимых передаточных отношений в машинах и приборах часто применяют сложные зубчатые механизмы, имеющие кроме входного и выходного колес несколько промежуточных колес, каждое из которых вращается вокруг своих осей. Применение сложных механизмов объясняется различными причинами. Например, оси входного и выходного колес расположены далеко друг от друга. В этом случае непосредственная передача вращения при помощи двух колес потребовала бы создания передачи с большими габаритами. В другом случае передаточное отношение может быть очень велико или очень мало, тогда удобно между входным и выходным колесами иметь промежуточные колеса со своими осями. Передавая вращение с входного колеса на промежуточные колеса и с них на выходное колесо, мы как бы последовательно отдельными ступенями изменяем скорость вращения звеньев, получая в результате требуемые передаточные отношения между входным и выходным колесами.
Таким образом, сложный механизм передачи можно разделить на отдельные части – ступени, каждая из которых представляет собой два колеса, образующих зубчатое зацепление. В соответствии с указанным бывают одно- и многоступенчатые передачи, по большей части двух- и трехступенчатые (рис.7). Количество ступеней равно числу зубчатых зацеплений, образованных зубчатыми колесами механизма. Одно колесо может входить в несколько ступеней (рис.8). Любая ступень может представлять собой цилиндрическую, коническую, червячную, глобоидную и т.д. передачу. На рис.8 показан многоступенчатый механизм, содержащий цилиндрические и конические ступени.
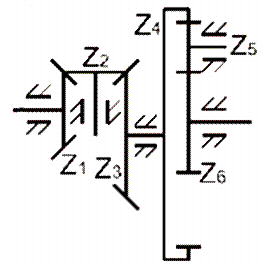
Рис.8. Многоступенчатая зубчатая передача
с паразитными колесами
Общее передаточное число (отношение) зубчатой передачи при последовательном соединении ступеней равно произведению передаточных чисел входящих в них ступеней. Для передачи на рис.7:
u 12 = u 12 ∙ u 34 = — z 2 z 1 ∙ — z 4 z 3 = z 2 z 1 ∙ z 4 z 3 . 
Зубчатые колеса, числа зубьев которых не влияют на общее передаточное отношение механизма, называются паразитными колесами . Для четырехступенчатой передачи, показанной на рис.8, передаточное число равно:
u 16 = u 12 ∙ u 23 ∙ u 45 ∙ u 56 = z 2 z 1 ∙ z 3 z 2 ∙ z 5 z 4 ∙ z 6 z 5 = z 3 z 1 ∙ z 6 z 4 . 
Знаки ступеней не учитываются так как передача включает кроме цилиндрических и конические ступени. Зубчатые колеса с числами зубьев z 2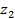 
и z 5 
являются паразитными, каждое из них входит в два зубчатых зацепления.
Планетарные зубчатые передачи
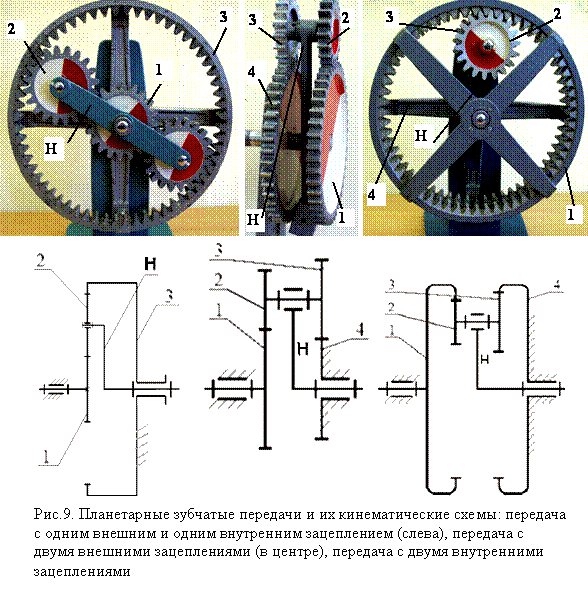
В некоторых многоступенчатых зубчатых передачах оси отдельных колес являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными механизмами (рис.9) , а с двумя и более степенями свободы – дифференциальными механизмами или просто дифференциалами. В этих механизмах колеса с подвижными осями вращения называются сателлитами (звено 2 на рис.9) , а звено, в котором установлены сателлиты — водилом. На схемах водило принято обозначать буквой Н. Зубчатые колеса, оси которых совпадают с осью вращения водила, назыаются центральными (звенья 1 и 4 на рис.9). Сателлиты бывают одновенцовые (левый рисунок) и многовенцовые.
Передаточное число планетарного механизма определяется по формуле:
u 1 H (4) =1- u 14 H ; u 14 H = u 12 H u 34 H ; 
где u 12 H , u 34 H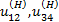 
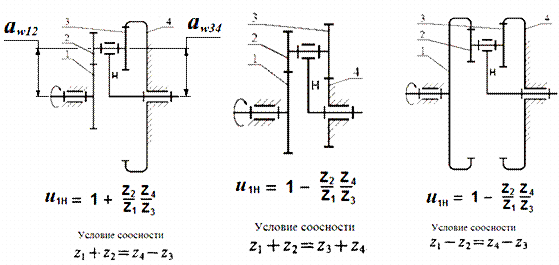
— передаточные числа ступеней (с учетом знаков) при остановленном водиле.
На рис.10 приведены формулы для определения передаточных чисел планетарных механизмов. Передаточные числа между подвижным центральным колесом и водилом связаны соотношением:
u H 1 = 1 u 1 H . 
Рис.10. Определение передаточных чисел планетарных механизмов
При выборе чисел зубьев колес планетарных зубчатых передач для них проверяются условия:
1. Условие соосности, обеспечивающее совпадение осей центральных зубчатых колес и водила: a w 12 = a w 34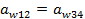 
(рис.10). Условия, приведенные на рис.10, получены для планетарных передач, зубчатые колеса которых имеют одинаковый модуль.
2. Условие соседства, обеспечивающее совместное размещение нескольких сателлитов по общей окружности в одной плоскости, без соприкосновения вершин зубьев соседних сателлитов:
sin π k > z c max +2 h a * z 1 + z 2 
где z c max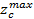 
— максимальное число зубьев зубчатого венца сателлита, k — число сателлитов
Условие соседства получено для планетарных передач, у которых сателлиты располагаются равномерно по окружности водила.
3. Условие сборки зубчатых колес передачи, определяющее возможность сборки передачи при использовании нескольких сателлитов:
z 1 u 1 H k 1+ k П =Ц 
где П— число полных поворотов водила 0,1,2,3. Ц— целое число 1,2,3, .
Макеты цилиндрических, конических, червячных, многоступенчатых и планетарных зубчатых механизмов.
Порядок выполнения работы
1. Получить задание и лабораторные макеты у преподавателя.
Каждый студент должен определить передаточное отношение и передаточное число пяти зубчатых передач:
1) цилиндрической зубчатой передачи;
2) конической зубчатой передачи;
3) зубчатой передачи со скрещивающимися осями;
4) многоступенчатой передачи с неподвижными осями колес;
5) планетарной зубчатой передачи.
2. Для каждой передачи:
2.1. Нарисовать кинематическую схему.
2.2. Дать полное название зубчатой передачи (определить ее тип и вид). Например, механизм, показанный на рис.7, называется цилиндрическая косозубая эвольвентная зубчатая передача.
2.3. Определить подвижность передачи по формуле Малышева для плоских механизмов.
2.4. Опытным путем определить передаточное отношение зубчатой передачи. Для этого посчитать число оборотов ведущего колеса соответствующее целому числу оборотов ведомого колеса.
2.5. Рассчитать передаточное число аналитически. Для чего посчитать числа зубьев колес передачи и по формулам найти передаточное число.
Для сложных зубчатых передач определить количество ступеней, указать паразитные колеса. Рассчитать передаточное число механизма, выразив его через числа зубьев колес.
2.6. Для планетарной передачи проверить выполнения условий соосности, соседства и сборки.
2.7. Составить сложную зубчатую передачу, соединив последовательно три из рассмотренных зубчатых передач. Нарисовать ее кинематическую схему и опредилить общее передаточное отношение.
2.8. Все результаты занести в отчет по лабораторной работе.
1. Перечислить звенья, входящие в простейшие зубчатые механизмы.
2. Перечислить звенья, входящие в сложные зубчатые механизмы.
3. Цель использования многоступенчатых передач.
4. Перечислить основные типы зубчатых передач.
5. Написать формулу для определения передаточного числа многоступенчатой зубчатой передачи.
6. Написать формулу для определения передаточного числа одноступенчатой зубчатой передачи.
7. В чем достоинства и недостатки прямозубых и косозубых зубчатых колес?
8. Чем планетарная зубчатая передача отличается от непланетарной ?
9. Зачем устанавливают несколько сателлитов в планетарном механизме?
10. Как определить передаточное число планетарной зубчатой передачи?
11. Какие условия проверяются для планетарной передачи? В чем их смысл?
12. Когда учитываются знаки передаточных чисел ступеней зубчатой передачи?
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Источник