Модуль момента силы тяжести fт лестницы

Максимальный угол наклона к вертикали, под которым может стоять лестница массой m, прислонённая к вертикальной гладкой стене и опирающаяся на горизонтальный шероховатый пол, равен Коэффициент трения между ножками лестницы и полом равен Лестницу установили, наклонив её именно под углом

Из приведённого ниже списка выберите два правильных утверждения.

1) Модуль силы реакции со стороны стены больше модуля силы трения между ножками лестницы и полом.

2) Модуль силы трения между лестницей и полом равен произведению коэффициента трения на модуль силы реакции со стороны стены.

3) Модуль силы трения между лестницей и полом равен произведению коэффициента трения на модуль силы тяжести.

4) Модуль силы тяжести меньше модуля силы реакции со стороны пола.

5) Момент силы трения относительно оси, проходящей через точку А, равен нулю.

На лестницу действуют силы, изображенные на рисунке.

1. Неверно. Так как лестница находится в равновесии, то В проекции на ось ОX:

2. Неверно. Сила трения равна

3. Верно. В проекции на ось OY: следовательно,

4. Неверно. См. пункт 3.

5. Верно. Линия действия силы трения проходит через точку А, поэтому M = 0.

Источник

К стене приставлена лестница массой 60 кг. Центр тяжести лестницы находится

Условие задачи:

К стене приставлена лестница массой 60 кг. Центр тяжести лестницы находится на расстоянии 1/3 длины от её верхнего конца. Какую горизонтальную силу нужно приложить к середине лестницы, чтобы её верхний конец не оказывал давления на стенку? Угол между лестницей и стеной равен 45°.

Задача №3.1.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

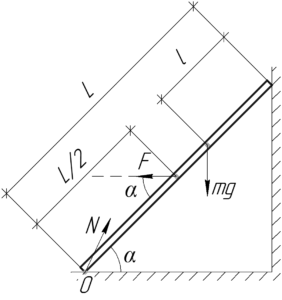
Если верхний конец не будет оказывать давления на стенку, то на этот конец не будут действовать никакие силы со стороны стенки (ни сила нормальной реакции, ни сила трения). Тогда на лестницу действуют лишь три силы: сила тяжести $mg$, сила реакции $N$ в точке O и горизонтальная сила $F$.

Лестница находится в равновесии. Запишем правило моментов (второе условие равновесия) относительно точки O – в этом случае момент силы реакции $N$ равен нулю, так как равно нулю её плечо.

\[F \cdot \frac <2>\cdot \sin \alpha – mg \cdot \left( \right) \cdot \cos \alpha = 0\]

Так как по условию $l=\frac<3>$, то:

\[F \cdot \frac <2>\cdot \sin \alpha – mg \cdot \left( <3>> \right) \cdot \cos \alpha = 0\]

\[\frac <2>\cdot \sin \alpha = \frac<<2mg>> <3>\cdot \cos \alpha \]

\[F = \frac<<4mg>> <3>\cdot ctg\alpha \]

Посчитаем ответ к задаче:

Ответ: 0,8 кН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Источник

Модуль момента силы тяжести fт лестницы

2018-07-15
Лестница массой 10 кг прислонена к стене под углом $60^< \circ>$ к полу. На какую максимальную высоту может подняться по этой лестнице человек массой 70 кг, чтобы лестница еще не сдвинулась? Коэффициенты трения между лестницей и полом, лестницей и стеной соответственно 0,4 и 0,5.

На лестницу действуют (рис.): силы тяжести $\vec_ <т>= M \vec$ и $\vec_ <т1>= m \vec$, силы нормальной реакции $\vec_<1>$ и $\vec_<2>$ и силы трения $\vec_<тp1>$ И $\vec_<тр2>, F_ <тр1>= \mu_ <1>N_<1>$ и $F_ <тр2>= \mu_<2>N_<2>$, так как берутся максимальные значения сил трения покоя.
Для равновесия лестницы должно выполняться условие:

или в проекции на оси х и у.

$N_ <2>— F_ <тр1>= 0$, (2)
$N_ <1>+ F_ <тр2>— Mg — mg = 0$. (3)

Из уравнений (2) и (3) получаем: $N_ <2>= \mu_<1>N_<1>$,

Для записи второго условия равновесия — правила моментов, выберем ось вращения, проходящую через точку А:

$Mg \frac <2>\cos \alpha + mga \cos \alpha — N_<2>l \sin \alpha — \mu_ <2>N_<2>l \cos \alpha = 0$,

$a = \frac<2 \mu_<1>(M + m)l( \mu_ <2>\cos \alpha + \sin \alpha ) — Ml(1 + \mu_ <1>\mu_ <2>) \cos \alpha > <2m \cos \alpha (1 + \mu_<1>\mu_ <2>)>$,

где $a = BA, a = 2,52 м; h = 4 \sin \alpha, h = 2,2 м$.

Источник

Модуль момента силы тяжести fт лестницы

2017-01-15
Лестница прислонена к наклонной стене, образующей угол $\beta$ с вертикалью (см. рис.). При каком коэффициенте трения лестницы о стенку возможно равновесие даже в том случае, когда пол идеально гладкий.

рис.1

рис.2
Прежде всего отметим, что лестница, прислоненная к вертикальной стенке, вообще не может находиться в равновесии, если нет трения о пол — она обязательно соскользнет по стенке. Более того, верхний конец лестницы при таком соскальзывании обязательно отделится от стенки раньше, чем лестница окажется на полу. Невозможность равновесия у вертикальной стенки на гладком полу очевидна из рис. 1: нормальная сила реакции стенки $\vec_<2>$ должна быть отлична от нуля так как иначе не будет уравновешен момент силы тяжести $m \vec$ относительно точки А; но сама сила $\vec_<2>$ может быть уравновешена только горизонтально направленной силой трения о пол.

А вот равновесие у наклонной шероховатой стенки возможно и на идеально гладком полу. На рис. 2 изображены силы, действующие на лестницу. Поскольку силы $m \vec$ и $\vec_<1>$ направлены вертикально, то в равновесии горизонтальные составляющие силы $\vec_<2>$ и $\vec_<тр>$ должны быть равны:

$N_ <2>\cos \beta = F_ <тр>\sin \beta$. (1)

Сила трения покоя $\vec_<тр>$ максимальна на пороге проскальзывания, когда ее значение равно $\mu N_<2>$. Из формулы (1) в этом случае находим

Формула (2) дает минимальное значение коэффициента трения $\mu$, при котором возможно равновесие у наклонной стенки с углом наклона $\beta$ в отсутствие трения о пол. При этом лестница как бы цепляется за шероховатую стенку, а другим концом давит на гладкий пол.

Обратим внимание на то, что условие равновесия лестницы не зависит ни от того, насколько наклонена сама лестница, ни от того, в каком месте приложена сила тяжести $m \vec$ и каково ее значение. Это значит, что лестница будет в равновесии и в том случае, если на ней в любом месте стоит человек.

Отметим, наконец, что условие (2) совпадает с выражением для предельного коэффициента трения, при котором возможно равновесие небольшого бруска, положенного на наклонную стенку.
Ответ: $\mu = ctg \beta$.

Источник

Физика

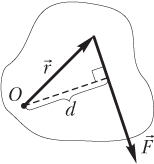
Момент силы относительно некоторой точки — это векторное произведение радиус-вектора r → , проведенного от этой точки к точке приложения силы, на силу F → :

Когда говорят о моменте силы относительно оси, проведенной через указанную точку, имеют в виду скалярную величину, равную проекции момента силы на указанную ось.

В Международной системе единиц момент силы измеряется в ньютонах, умноженных на метр (1 Н ⋅ м).

Модуль момента силы вычисляется по формуле

где r — длина радиус-вектора, проведенного от оси вращения к точке приложения силы; F — модуль приложенной к телу силы; α — угол между векторами r → и F → .

Точка O , относительно которой рассчитывается момент приложенной к телу силы F → , может находиться как на самом теле (рис. 4.3), так и вне его (рис. 4.4). Радиус-вектор r → проводят от точки O к точке приложения силы F → .

На рисунках показано, как правильно определять угол α между указанными векторами в случаях их различного взаимного расположения.

Плечо силы — кратчайшее расстояние от линии действия силы (продолжение вектора силы в пространстве) до точки O (рис. 4.5).

Плечо силы представляет собой произведение

где r — длина радиус-вектора, проведенного от оси вращения к точке приложения силы; α — угол между векторами r → и F → .

Модуль момента силы может быть записан в виде:

где d — плечо силы; F — модуль приложенной силы.

Направление момента силы определяют по правилу правого винта : направление момента M → совпадает с поступательным движением правого винта, если его рукоятку вращать от r → (радиус-вектор, проведенный от оси к точке приложения силы) к F → (приложенная сила) по наименьшему углу.

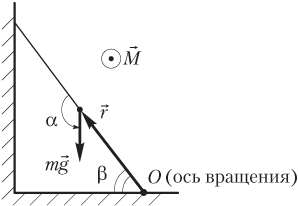
Пример 10. Однородная лестница длиной 12 м и массой 24 кг приставлена к стене и образует с полом угол 60°. Определить момент силы тяжести относительно оси, проходящей через нижний конец лестницы параллельно ее ступенькам.

Решение . Лестница является однородной; следовательно, центр тяжести лестницы находится в ее середине.

На рисунке показаны:

сила тяжести, действующая на лестницу;

радиус-вектор, проведенный от оси вращения к точке приложения силы;

угол α между указанными векторами.

Модуль момента силы тяжести относительно указанной оси определяется по формуле

где F = mg — модуль силы тяжести; r = l /2 — модуль радиус-вектора; l — длина лестницы; α = ( 90 ° + β ) — угол между вектором силы тяжести и радиус-вектором точки ее приложения относительно заданной оси; β — угол между лестницей и полом.

С учетом выражений для модулей силы тяжести, радиус-вектора и угла между ними формула для расчета модуля момента силы тяжести в явном виде выглядит следующим образом:

M = m g l 2 sin 150 ° .

M = 24 ⋅ 10 ⋅ 12 2 ⋅ 0,5 = 0,72 ⋅ 10 3 Н ⋅ м = 0,72 кН ⋅ м.

Направление момента силы тяжести определяется по правилу правого винта: вращаем правый винт от радиус-вектора к вектору силы по наименьшему углу (против часовой стрелки); направление поступательного движения винта («к нам») совпадает с направлением данного момента; указанное направление на рисунке обозначено ⊙ M → .

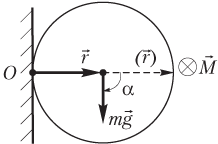
Пример 11. Пластина в форме однородного диска площадью 314 см 2 закреплена на горизонтальной оси таким образом, что диаметр диска, проведенный через точку крепления, горизонтален и перпендикулярен оси вращения. Найти величину момента силы тяжести, если масса пластины составляет 300 г.

Решение . Пластина является однородной; следовательно, центр ее тяжести находится в геометрическом центре круга.

На рисунке показаны:

сила тяжести, действующая на пластину;

радиус-вектор, проведенный от оси вращения к точке приложения силы;

угол α между указанными векторами.

Модуль момента силы тяжести относительно указанной оси определяется по формуле

где F = mg — модуль силы тяжести; r = R — модуль радиус-вектора; R — радиус круга; α = 90° — угол между вектором силы тяжести и радиус-вектором точки ее приложения относительно заданной оси.

С учетом выражений для модулей силы тяжести, радиус-вектора и угла между ними формула для расчета модуля момента силы тяжести приобретает вид:

M = m g R sin 90 ° .

Определим радиус пластины, используя выражение для площади круга:

Отсюда следует, что радиус круга определяется по формуле

Подставим данное выражение в формулу для вычисления модуля момента силы тяжести:

M = m g S π sin 90 °

и рассчитаем его значение:

M = 300 ⋅ 10 − 3 ⋅ 10 314 ⋅ 10 − 4 π ⋅ 1 = 0,3 Н ⋅ м = 300 мН ⋅ м.

Направление момента силы тяжести определяется по правилу правого винта: вращаем правый винт от радиус-вектора к вектору силы по наименьшему углу (по часовой стрелке); направление поступательного движения винта («за плоскость чертежа», «от нас») совпадает с направлением данного момента; указанное направление на рисунке обозначено ⊗ M → .

Пример 12. Палочка в виде тонкого однородного цилиндра длиной 60 см и площадью поперечного сечения 3,0 см 2 закреплена на оси вращения верхним концом. Нижний конец палочки опущен в воду плотностью 1,0 г/см 3 и погружен в нее на 1/3 длины. Вычислить модуль момента силы Архимеда, действующей на палочку, относительно горизонтальной оси, проходящей перпендикулярно палочке через ее верхний конец, при отклонении палочки от вертикали на 30°.

Решение . Сила Архимеда действует на погруженную в воду часть палочки и приложена к середине погруженной части.

На рисунке показаны:

сила Архимеда, действующая на погруженную в воду часть палочки;

радиус-вектор, проведенный от оси вращения к точке приложения силы;

угол α между указанными векторами.

Модуль момента силы Архимеда относительно указанной оси определяется по формуле

где F = F A = ρ 0 g V ′ — модуль силы Архимеда; ρ 0 — плотность воды; g — модуль ускорения свободного падения; V ′ = 1 3 V — объем погруженной части палочки; V — объем палочки; r = 5 6 l — модуль радиус-вектора; l — длина палочки; α = 180 ° − 30 ° = 150 ° — угол между вектором силы Архимеда и радиус-вектором точки ее приложения относительно заданной оси.

С учетом выражений для модулей силы Архимеда, радиус-вектора и угла между ними формула для расчета модуля момента силы Архимеда приобретает вид:

M = ( 1 3 ρ 0 g V ) ( 5 6 l ) sin 150 ° = 5 18 ρ 0 g V l sin 30 ° .

Объем палочки представим в виде произведения

и подставим в выражение для расчета модуля момента силы Архимеда:

M = 5 18 ρ 0 g S l 2 sin 30 ° ,

где S — площадь поперечного сечения палочки.

M = 5 18 ⋅ 1,0 ⋅ 10 3 ⋅ 10 ⋅ 3,0 ⋅ 10 − 4 ( 60 ⋅ 10 − 2 ) 2 ⋅ 0,5 = 0,15 Н ⋅ м.

Направление момента силы Архимеда определяется по правилу правого винта: вращаем правый винт от радиус-вектора к вектору силы по наименьшему углу (против часовой стрелки); направление поступательного движения винта («к нам») совпадает с направлением данного момента; указанное направление на рисунке обозначено ⊙ M → .

Источник

Читайте также: Монтаж деревянной лестницы по бетону