Линейные электрические цепи

Электрической цепью называется совокупность элементов, образующих пути для прохождения электрического тока. Электрическая цепь состоит из активных и пассивных элементов.

Активными элементами считаются источники электрической энергии (источники напряжения и тока), к пассивным элементам относятся резисторы, катушки индуктивности, электрические конденсаторы.

Количественные характеристики элементов электрической цепи называются ее параметрами . Например, параметрами источника постоянного напряжения являются его ЭДС и внутреннее сопротивление. Параметром резистора служит его сопротивление катушки — ее индуктивность L и конденсатора — емкость С.

Напряжение или ток, подводимые к цепи, будем называть воздействующим или входным сигналом . Воздействующие сигналы можно рассматривать как различные функции времени, изменяющиеся по некоторому закону z ( t ) . Например, z ( t ) может быть постоянной величиной, изменяться во времени по периодическому закону или иметь апериодический характер.

Напряжения и токи, возникающие под влиянием внешнего воздействия в интересующей нас части электрической цепи и также являющиеся функциями времени х( t ) , будем называть реакцией (откликом) цепи или выходным сигналом .

Любой пассивный элемент реальной электрической цепи в той или иной степени обладает активным сопротивлением, индуктивностью и емкостью. Однако, чтобы облегчить изучение процессов в электрической цепи и ее расчет, реальная цепь заменяется идеализированной, состоящей из отдельных пространственно разделенных элементов R, L, С.

При этом считается, что проводники, соединяющие элементы цепи, не обладают активным сопротивлением, индуктивностью и емкостью. Такая идеализированная цепь называется цепью с сосредоточенными параметрами , и основанные на ней расчеты дают во многих случаях хорошо подтверждаемые опытом результаты.

Э лектрические цепи с постоянными параметрами — это такие такие цепи, в которых сопротивления резисторов R, индуктивность катушек L и емкость конденсаторов С являются постоянными, не зависящими от действующи в цепи токов и напряжений. Такие элементы называются линейными .

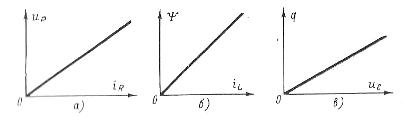
Если сопротивление резистора R не зависит от тока, то линейная зависимость между падением напряжения и током выражается законом Ома ur = R х i_r, а вольт-амперная характеристика резистора (представляет собой прямую линию (рис. 1,а).

Если индуктивность катушки не зависит от величины (протекающего в ней тока, то потокосцепление самоиндукции катушки ψ прямо пропорционально этому току ψ = L х i_l (рис. 1,б).

Наконец, если емкость конденсатора С не зависит от приложенного к обкладкам напряжения uc то заряд q, накопленный на пластинах, и напряжение u_c связаны между собой линейной зависимостью графически показанной на рис. 1, в .

Рис. 1. Характеристики линейных элементов электрической цепи: а — вольт-амперная характеристика резистора, б — зависимость потокосцепления от тока в катушке, в — зависимость заряда конденсатора от напряжения на нем.

Линейность сопротивления, индуктивности и емкости носит условный характер, так как в действительности все реальные элементы электрической цепи являются нелинейными. Так, при прохождении тока через резистор последний нагревается и его сопротивление изменяется.

Чрезмерное увеличение тока в катушке с ферромагнитным сердечником может несколько изменит ее индуктивность. В той или иной степени изменяется емкость конденсаторов с различными диэлектриками в зависимости от приложенного напряжения.

Однако в нормальном рабочем режиме элементов эти изменения обычно столь незначительны, что при расчетах могут не приниматься во внимание и такие элементы электрической цепи считаются линейными.

Транзисторы, работающие в режимах, когда используются прямолинейные участки их вольт-амперных характеристик, также условно могут рассматриваться как линейные устройства .

Электрическая цепь, состоящая из линейных элементов, называется линейной электрической цепью . Линейные цепи характеризуются линейными уравнениями для токов и напряжений и заменяются линейными схемами замещения. Линейные схемы замещения составляются из линейных пассивных и активных элементов, вольтамперные характеристики которых линейны. Для анализа процессов в линейных электрических цепях используются законы Кирхгофа.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Активные линейные цепи

Литература: [Л.1], стр. 205-206, 226-228

Типичным примером активной цепи является усилитель, собранный на n-p-n транзисторе с общим эмиттером. Если нагрузкой усилителя служит R-цепь, то такой усилитель является апериодической активной цепью, а если нагрузкой служит колебательный контур – частотно-избирательной активной цепью.

На рис. 5.10 представлена упрощенная принципиальная схема частотно-избирательной активной цепи. При достаточно малой амплитуде входного сигнала такую цепь можно считать линейной (линейным усилителем малых сигналов). Этот случай мы и рассмотрим.

Для определения характеристик рассматриваемой активной цепи составим ее эквивалентную схему. Транзистор можно представить в

виде источника тока управляемого напряжением . Величина тока в этом случае составит

, (5.69)

где – крутизна характеристики транзистора (крутизна управления), имеющая размерность . Как известно, источник тока можно представить как параллельное соединение идеального источника и внутреннего сопротивления, в качестве которого выступает внутреннее сопротивление транзистора . Тогда эквивалентная схема рассматриваемой цепи принимает вид (рис. 5.11).

Так же, как и для пассивной цепи (параллельного контура) комплексный коэффициент передачи:

.

совпадает с комплексным сопротивлением . Вместе с тем, для рассматри-ваемой цепи комплексная

проводимость определяется выражением

, (5.70)

где – эквивалентное сопротивление контура с учетом внутреннего сопротивления транзистора. Сравнение (5.70) с (5.59) показывает, что комплексный коэффициент передачи рассматриваемой цепи описывается выражением (5.60) с той лишь разницей, что вместо собственного сопротивления параллельного контура здесь выступает

. (5.71)

Очевидно, исходя из эквивалентной схемы, добротность рассматриваемого усилителя составит величину

. (5.72)

Так как , то включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности, что объясняется шунтирующим свойством транзистора.

Аналогично комплексный коэффициент передачи как функция удвоенной относительной расстройки ε описывается выражением

, (5.73)

а амплитудно-частотная и фазо-частотная характеристики – соответственно выражениями:

, (5.74)

. (5.75)

Полоса пропускания рассматриваемого усилителя определяется в соответствии с (5.54), где вместо фигурирует

. (5.76)

Очевидно, так как включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности до , это в свою очередь обуславливает расширение полосы пропускания.

Контрольные вопросы к главе 5

1. Приведите классификацию радиотехнических цепей.

2. Чем отличаются линейные цепи от нелинейных?

3. Как описывается импульсная характеристика цепи? Что такое оператор преобразования сигнала линейной цепью?

4. Поясните смысл амплитудно-частотной характеристики и чем она отличается от фазо-частотной характеристики?

5. Какие линейные цепи называются инерционными?

6. Перечислите методы анализа преобразования сигналов линейными цепями.

7. Сравните классический и временной методы преобразования сигнала линейной цепью.

8. Что есть общего между спектральным и операторным методами?

9. Какие радиотехнические цепи называются пассивными апериодическими цепями?

10. Приведите примеры пассивных частотно-избирательных цепей и перечислите их характеристики.

11. Какие линейные цепи относятся к активным цепям?

12. Приведите характеристики частотно-избирательной цепи.

Глава 6. Преобразование детерминированных

сигналов линейными цепями

Рассмотренные выше математические модели различных сигналов и линейных цепей позволяют перейти к рассмотрению задач прохождения сигналов через линейные цепи. При этом, целесообразно все многообразие задач разделить на две группы. К первой группе следует отнести задачи преобразования первичных, т.е. видеосигналов, как одиночных, так и периодических. Вторая группа объединяет задачи анализа прохождения модулированных сигналов через линейные цепи.

В общем случае задача анализа прохождения сигналов через линейные цепи формулируется следующим образом. Задан входной сигнал и его характеристики (временные, спектральные, операторные). Входной сигнал поступает на линейную цепь (рис. 5.) с известными характеристиками (временными, спектральными, операторными). Необходимо найти соответствующие характеристики входного сигнала. При этом в соответствии с целями анализа в большинстве случаев нет необходимости находить все характеристики выходного сигнала, а ограничиться некоторыми из них, например, формой выходного сигнала или его спектром . Это в свою очередь, определяет выбор метода анализа.

Ввиду многообразия задач преобразования детерминированных сигналов линейными цепями ниже будут рассмотрены некоторые из них, освоение методики решения которых позволит решать и более сложные задачи.

Источник: Медиченко М.П., Литвинов В.П. Радиотехнические цепи и сигналы: Учебное пособие. – М.: Изд-во МГОУ, 2011.

Источник

Активная и пассивная электрическая цепь

Вы будете перенаправлены на Автор24

Элементы электроцепей могут быть соединены в схемах за счет различных способов. Для каждого из них существуют некоторые закономерности, установленные такими учеными, как Ом и Кирхгоф.

Графическое изображение реальной электроцепи условными символами считается электрической схемой. Она, в свою очередь, считается идеализированной цепью, служащей в качестве расчетной модели реальной цепи и иногда называемой эквивалентной схемой замещения. Она по возможности должна отображать реальные процессы, осуществляемые в действительности.

Понятие электрической цепи и ее элементов

Электрической цепью считается комплекс электротехнических устройств, образующих путь к прохождению электротока и ориентированных на передачу, распределение и взаимное преобразование электрической и иных разновидностей энергии.

Готовые работы на аналогичную тему

Электромагнитные процессы, протекающие в устройствах электроцепи, могут описать такие понятия, как электродвижущая сила, напряжение и ток.

Электрические цепи называют цепями постоянного тока, когда в них получение электрической энергии, а также её передача и преобразование осуществляются при условии неизменности во времени тока и напряжения.

Базовыми элементами электрической цепи будут являться источники и приемники электроэнергии, которые соединяют между собой провода.

Каждая электроцепь включает в себя разнообразные устройства и объекты, отвечающие за формирование путей для прохождения электрического тока. Условным образом все элементы электроцепи разделяются на три составные части:

• источники питания, вырабатывающие электроэнергию;
• элементы, преобразующие электричество в прочие виды энергии (приемники);
• передающие устройства (провода и иные установки, отвечающие за обеспечение качества и уровня напряжения).

В электроцепях соединение потребителей может быть комбинированным, последовательным, параллельным.

Активные элементы электрической цепи

Элементы в составе электрических цепей существуют в формате активности и пассивности. В качестве активных считаются источники электроэнергии.

Источники, подобно всем остальным элементам электрической цепи, могут характеризоваться как линейные и нелинейные. Линейным свойственна линейная внешняя характеристика. При условии постоянства напряжения на выходе источника и его независимости от тока в нагрузке, такой источник называют источником ЭДС.

Базовым признаком активных составляющих выступает их способность отдачи электрической энергии. Источники тока и ЭДС называют идеальными для электрической энергии, что обусловлено отсутствием потерь энергии в них, поскольку их проводимость и сопротивление считаются бесконечными:

В ситуации, когда потери электроэнергии внутри источника не компенсируются, ему свойственна наклонная внешняя характеристика. Такие источники будут называться реальными.

Пассивные элементы электрической цепи

Пассивными элементами считают разновидности потребителей и накопителей электроэнергии. Существует многополюсная аппаратура, чье функционирование основано на базе двухполюсных элементов. Все активные элементы электроцепи могут существовать как в независимом, так и в зависимом формате.

К первой категории относят источники тока и напряжения (идеализированный элемент в цепи с нулевым значением внутреннего сопротивления). Источник тока также представляет собой совершенный элемент с независимостью тока от напряжения на зажимах, со стремлением значения внутреннего сопротивления к бесконечности.

Зависимые источники напряжения и тока такими считаются при условии зависимости указанных величин от параметров напряжения и тока на ином участке цепи. Типичными представителями выступают электролампы и транзисторы, чье функционирование происходит в режиме линейности.

Главные пассивные элементы электроцепи представляют резисторы, индуктивные катушки и конденсаторы, с помощью которых осуществляется регулирование параметров тока и напряжения на отдельно взятых участках.

Резистивное сопротивление относят к идеализированным элементам в цепи. Его базовым свойством считают необратимое энергетическое рассеивание. Зависимость напряжения и тока резистивного сопротивления выражают формулы:

При этом $R$ представляет сопротивление (измеряется в Омах), а $G$ выступает проводимостью (единица измерения – сименсы). Данные величины будут соотноситься в формуле:

Индуктивность считают еще и коэффициентом пропорциональности. Ёмкостные элементы (то есть конденсаторы) обладают свойством накопления энергии электрического поля. Показатель линейной емкости является линейной зависимостью между зарядом и напряжением, выраженной формулой:

Источник