Лестница мебиуса что это такое

Лента Мебиуса — удивительное открытие

Практически все знают, как выглядит символ бесконечности, напоминающий перевернутую восьмерку. Этот знак называют еще «лемниската», что с древнегреческого означает лента. Представьте себе, что символ бесконечности очень похож на реально существующую математическую фигуру. Знакомьтесь, Лента Мебиуса!

Что такое Лента Мебиуса?

Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Петля Мебиуса — это петля с одной поверхностью и одним краем.

Чтобы понять, о чем идет речь, и как такое может быть, возьмите лист бумаги, вырежьте полоску прямоугольной формы и в момент соединения ее концов перекрутите на 180 градусов один из них, после чего соедините. Разобраться в том, как сделать ленту Мебиуса поможет картинка ниже.

Что же такого примечательного в ленте Мебиуса?

Лента Мебиуса – пример неориентируемой односторонней поверхности с одним краем в обычном трёхмерном Евклидовом пространстве. Большинство предметов являются ориентируемыми, имеющими две стороны, например, лист бумаги.

Как тогда лента Мёбиуса может быть неориентируемой, односторонней поверхностью — скажете вы, ведь бумага, из которой она сделана имеет две стороны. А вы попробуйте взять маркер и заполнить цветом одну из сторон ленты, в конечном итоге вы упретесь в начальную позицию, причем вся лента окажется целиком закрашенной, что подтверждает наличие у нее всего одной стороны.

Чтобы поверить в то, что у петли Мебиуса всего один край – проведите пальцем по одному из граней ленты не прерываясь, и Вы точно так же, как и в случае с раскрашиванием, упретесь в точку, с которой начали движение. Удивительно, не правда ли?

Изучением ленты Мёбиуса и множества других интересных объектов занимается – топология, раздел математики, который исследует неизменные свойства объекта при его непрерывной деформации – растяжении, сжатии, изгибе, без нарушения целостности.

Открытие Августа Мебиуса

«Отцом» открывателем этой необычной ленты признан немецкий математик Август Фердинанд Мебиус, ученик Гаусса, написавший не одну работу по геометрии, но прославившийся преимущественно открытием односторонней поверхности в 1858 году.

Удивительным является тот факт, что ленту с одной поверхностью в тот же самый 1858 год открыл другой ученик Гаусса – талантливый математик Иоганн Листинг, придумавший термин «топология» и написавший серию основополагающих трудов по этому разделу математики. Однако свое название необычная лента все же получила по фамилии Мебиуса.

Есть расхожее мнение, что прообразом модели «бесконечной петли» стала неверно сшитая лента служанкой профессора Августа Мебиуса.

На самом деле, лента была открыта давным-давно еще в древнем мире. Одним из подтверждений служит находящаяся во Франции, в музее города Арль древнеримская мозаика с такой же перекрученной лентой. На ней нарисован Орфей, очаровывающий зверей звуками арфы. На фоне неоднократно изображен орнамент с перекрученной лентой.

«Магия» ленты Мебиуса

1. Несмотря на кажущееся наличие у листа Мебиуса двух сторон, на самом деле сторона всего одна, и раскрасить в два цвета ленту не получится.
2. Если ручкой или карандашом начертить по всей длине петли линию, не отрывая руку от листа, то грифель в конечном итоге остановится в точке, с которой Вы начали чертить линию;
3. Примечательные опыты получаются при разрезании ленты, способные удивить, как взрослого, так и ребенка в особенности.

• Для начала склеим ленту Мебиуса, как было рассказано ранее. Затем разрежем ее вдоль по всей длине ровно посередине, как показано ниже:

Вас порядком удивит результат, ведь вопреки ожиданиям в руках останется не два отрезка ленты, и даже не два отдельных круга, но другая, еще более длинная лента. Это уже будет не лента Мебиуса, перекрученная на 180 градусов, а лента с поворотом на 360 градусов.

• Теперь проведем другой эксперимент – сделаем еще одну петлю Мебиуса, после чего отмерим 1/3 ширины ленты и отрежем по этой линии. Результат поразит вас еще больше – в руках останутся две отдельные ленты разных размеров, соединенные вместе, как в цепочке: одна маленькая лента, и более длинная вторая.

У меньшей ленты Мёбиуса будет 1/3 от изначальной ширины ленты, длина L и поворот на 180 градусов. У второй более длинной ленты будет также ширина 1/3 от начальной, но длина 2L, а поворот на 360 градусов.

• Можно и дальше продолжать эксперимент, разрезая получившиеся ленты на еще более узкие, результат увидите сами.

Зачем нужна петля Мебиуса? Применение

Лента Мебиуса – вовсе не абстрактная фигура, нужная лишь для целей математики, она нашла применение и в реальной повседневной жизни. По принципу этой ленты функционирует в аэропорту лента, передвигающая чемоданы из багажного отделения. Такая конструкция позволяет ей служит дольше в связи с равномерным изнашиванием. Открытие Августа Мебиуса повсеместно исполбьзуется в станкостроении. Конструкцию используют для большего времени записи на пленку, а также в принтерах, использующих ленту при распечатке.

Благодаря своей наглядности, петля Мебиуса дает возможность делать современным ученым все новые и новые открытия. С момента обнаружения удивительных свойств петли по всему миру прокатилась волна новых запатентованных изобретений. Например, значительное улучшение свойств магнитных сердечников, изготовленных из ферро-магнитной ленты, намотанных по способу Мебиуса.

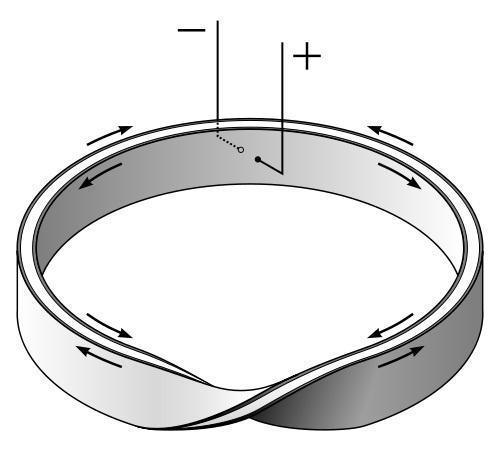
Н. Тесла получил патент на многофазную систему переменного тока, использовав намотку катушек генератора по типу петли Мебиуса.

Американский ученый Ричард Дэвис сконструировал нереактивный резистор Мебиуса — способный гасить реактивное (емкостное и индуктивное) сопротивление, не вызывая элекстромагнитных помех.

Лента Мебиуса – широкое поле для Вдохновения

Сложно оценить важность значения открытия петли Мебиуса, которое вдохновило не только большое множество ученых, но и писателей, художников.

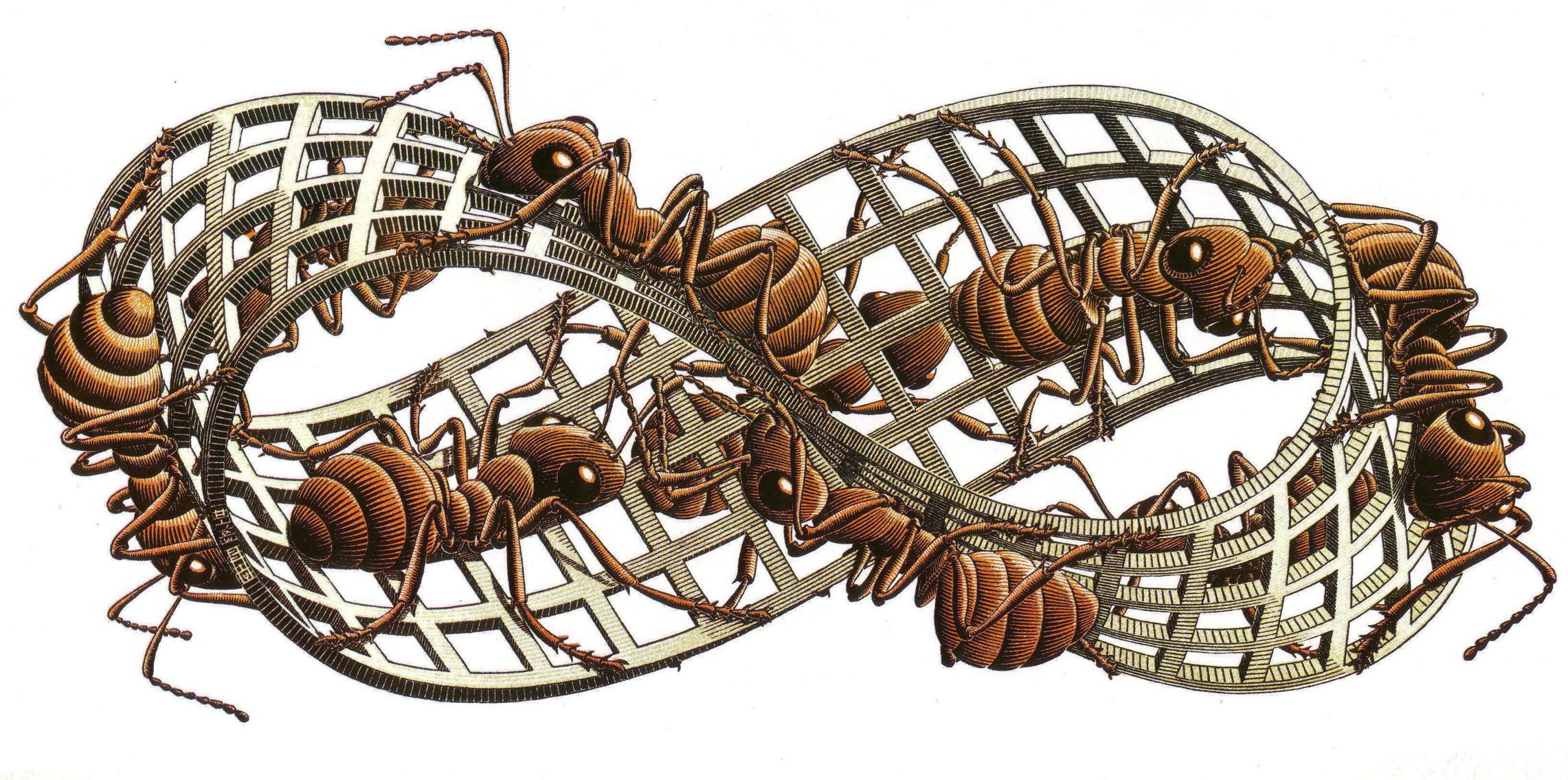
Самой известной работой, посвященной ленте Мебиуса считается картина Moebius Strip II, Red Ants или Красные Муравьи голландского художника-графика Маурица Эшера. На картине представлены муравьи, карабкающиеся по петле Мебиуса с обеих сторон, на самом деле сторона всего одна. Муравьи ползут по бесконечной петле друг за другом по одной и той же поверхности.

Художник черпал свои идеи из статей и трудов по математике, он был глубоко увлечен геометрией. В связи с чем на его литографиях и гравюрах часто присутствуют различные геометрические формы, фракталы, потрясающие оптические иллюзии.

До сих пор интерес к петле Мебиуса находится на очень высоком уровне, даже спортсмены ввели одноименную фигуру высшего лыжного пилотажа.

По произведению «Лента Мёбиуса» писателя фантаста Армина Дейча снят не один фильм. В форме петли Мебиуса создается огромное множество украшений, обуви, скульптур и многих других предметов и форм.

Лист Мебиуса наложил отпечаток на производство, дизайн, искусство, науку, литературу, архитектуру.

Умы многих людей волновала схожесть формы молекулы ДНК и петли Мебиуса. Существовала гипотеза, которую выдвинул советский цитолог Навашин, что форма кольцевой хромосомы по строению аналогична ленте Мебиуса. На эту мысль ученого натолкнул тот факт, что кольцевая хро­мосома, размножаясь, превращается в более длинное кольцо, чем в самом начале, или в два небольших кольца, но как в цепи продетых одно в другое, что очень напоминает выше описанные опыты с листом Мебиуса.

В 2015 году группа ученых из Европы и США смогла закрутить свет в кольцо Мёбиуса. В научном опыте ученые использовали оптические линзы, и структурированный свет — сфокусированный лазерный луч с преопределенными интенсивностью и поляризацией в каждой точке своего движения. В итоге были получены световые ленты Мебиуса.

Есть еще одна более масштабная теория. Вселенная – это огромная петля Мебиуса. Такой идеи придерживался Эйнштейн. Он предположил, что Вселенная замкнута, и космический корабль, стартовавший из определенной ее точки и летящий все время прямо, возвратится в ту же самую точку в пространстве и времени, с которой и началось его движение.

Пока это всего лишь гипотезы, у которых есть как сторонники, так и противники. Кто знает, к какому открытию подведет ученых, казалось бы, такой простой объект, как Лента Мебиуса.

Источник

Лестница Мебиуса — Möbius ladder

В теории графов , то Мёбиусова лестница М _п является кубическим циркулянтом графа с четным числом п вершин, образованным из п — цикл добавления ребер ( так называемый «ступеньку») , соединяющей противоположные пары вершин в цикле. Он назван так потому, что (за исключением M ₆ = K _3,3 ) M _n имеет ровно n / 2 4-циклов, которые соединяются вместе своими общими ребрами, образуя топологическую ленту Мёбиуса . Лестницы Мебиуса были названы и впервые изучены Гаем и Харари ( 1967 ).

СОДЕРЖАНИЕ

Характеристики

Каждая лестница Мёбиуса является неплоским графом с вершинами , что означает, что ее нельзя нарисовать без пересечений на плоскости, но удаление одной вершины позволяет нарисовать оставшийся граф без пересечений. Лестницы Мебиуса имеют пересечение номер один и могут быть вложены без пересечений на торе или проективной плоскости . Таким образом, они являются примерами тороидальных графов . Ли (2005) исследует вложения этих графов на поверхности более высокого рода.

Лестницы Мебиуса являются вершинно-транзитивными — у них есть симметрии, переводящие любую вершину в любую другую вершину — но (опять же, за исключением M ₆ ) они не являются реберно-транзитивными . Ребра цикла, из которого образована лестница, можно отличить от ступенек лестницы, потому что каждое ребро цикла принадлежит одному 4-циклу, в то время как каждая ступень принадлежит двум таким циклам. Следовательно, не существует симметрии, переводящей ребро цикла в ребро ступени или наоборот.

При п ≡ 2 ( по модулю 4) , М _п является двудольным . Когда n ≡ 0 (mod 4) , он не является двудольным. Конечные точки каждой ступени находятся на четном расстоянии друг от друга в начальном цикле, поэтому добавление каждой ступени создает нечетный цикл. В этом случае, поскольку граф является 3-регулярным, но не двудольным, по теореме Брукса он имеет хроматическое число 3. Де Майер и Ной (2004) показывают, что лестницы Мебиуса однозначно определяются своими полиномами Тутте .

Лестница Мебиуса M ₈ имеет 392 опорных дерева ; он и M ₆ имеют самые остовные деревья среди всех кубических графов с одинаковым числом вершин. Однако кубический граф с 10 вершинами с наибольшим количеством остовных деревьев — это граф Петерсена , который не является лестницей Мёбиуса.

Эти многочлены TUTTE из лестниц Мёбиуса может быть вычислены с помощью простого рекуррентного соотношения .

График миноров

Лестницы Мебиуса играют важную роль в теории миноров графов . Самым ранним результатом этого типа является теорема Клауса Вагнера ( 1937 ) о том, что графы без минора K ₅ могут быть сформированы путем использования операций кликовой суммы для объединения плоских графов и лестницы Мёбиуса M ₈ ; по этой причине M ₈ называется графом Вагнера .

Губсер (1996) определяет почти планарный граф как непланарный граф, для которого каждый нетривиальный минор является плоским; он показывает, что трехсвязные почти плоские графы являются лестницами Мебиуса или членами небольшого числа других семейств, и что другие почти планарные графы могут быть сформированы из них с помощью последовательности простых операций.

Махарри (2000) показывает, что почти все графы, не имеющие минорного куба, могут быть получены с помощью последовательности простых операций из лестниц Мебиуса.

Химия и физика

Вальба, Ричардс и Халтивангер (1982) впервые синтезировали молекулярные структуры в форме лестницы Мебиуса, и с тех пор эта структура вызывает интерес в химии и химической стереографии, особенно ввиду лестничной формы молекул ДНК. Имея в виду это приложение, Флапан ( 1989 ) изучает математические симметрии вложений лестниц Мебиуса в R 3 . В частности, как она показывает, любое трехмерное вложение лестницы Мебиуса с нечетным числом ступенек является топологически киральным : его нельзя преобразовать в свое зеркальное отображение путем непрерывной деформации пространства, не пропуская одно ребро через другое. С другой стороны, все лестницы Мебиуса с четным числом ступенек имеют вложения в R 3, которые можно деформировать в их зеркальное отображение.

Лестницы Мебиуса также использовались в качестве формы сверхпроводящего кольца в экспериментах по изучению влияния топологии проводника на взаимодействие электронов.

Комбинаторная оптимизация

Лестницы Мебиуса также использовались в информатике как часть подходов к целочисленному программированию для решения задач упаковки множеств и линейного упорядочения. Определенные конфигурации в рамках этих задач могут использоваться для определения граней многогранника, описывающего релаксацию задачи линейным программированием ; эти фасеты называются лестничными ограничениями Мёбиуса.

Источник