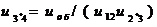Кинематический расчет по ступеням передачи

Кинематический расчет передачи

1. Определяют приближенное значение общего передаточного числа:

; (23.5)

и разбивают его по ступеням: , (23.6)

где С_тr – коэффициент, определяемый из оптимизации по одному из параметров (габаритным размерам, инерционности, точности и др.); индекс «тr» у коэффициента С_тr обозначает, что передача вращения выполняется от шестерни z_т к колесу z_r; k – количество ступеней передачи.

Для цилиндрических зубчатых передач коэффициент С_тr принимают:

· из условия минимума габаритных размеров для развернутой схемы (оптимальный вариант, когда колеса и шестерни обоих ступеней имеют одинаковые диаметры) при двухступенчатой передаче (k = 2) С₁₂ = 1,2; при трехступенчатой (k = 3) С₁₂ = 1,3, С₂‘₃ = 1, а для соосных передач при k = 2 С₁₂ = С₂₃ = 1. Передаточное число последней ступени находят при k = 2 из выражения ; при k = 3 – из выражения .

· из условия минимума инерционности у быстроходных реверсивных приводов при k = 2 С₁₂ = 0,6¸0,95; при k = 3 С₁₂ = 0,5¸0,8, С_2’3 = 0,9¸0,95.

Если на выходе стоит передача винт-гайка, то п_вых – частота вращения вала на выходе из редуктора равная частоте вращения винта (гайки, об/мин): , (23.7) где р – шаг, мм; z – число заходов резьбы; u – скорость, м/с.

У высокоточных передач для обеспечения соответствующей точности необходимы высокие требования к последней ступени (высокая точность и большое передаточное число и > 100). В этом случае точность привода будет определяться последней ступеней, а погрешности предыдущих ступеней не окажут на нее существенного влияния.

2. Выбирают число зубьев каждого колеса в паре:

суммарное число зубьев z_S = z₁ + z₂: для зубчатых колес с однородной структурой z_S – 80¸90; для мелкомодульных (т

Возможен другой вариант кинематического расчета, когда число зубьев шестерни z₁ = 17¸25 и z₂ = z₁ × и₁₂. При числе зубьев, меньшем z = 17, для устранения подрезания необходимо выполнить модификацию профилей (смещение контура), но z₁ брать не менее 12.

Силовой расчет передачи

1. Вычисляют номинальный вращающий момент двигателя (Н × мм):

2. Определяют расчетный вращающий момент на каждом валу:

где К_дин – коэффициент динамичности внешней нагрузки; П_i – потери в подшипниках.

Конструкция редуктора

Для удобства сборки и разборки корпус редуктора делают составным, обычно из двух частей (рис. 23.3): основания О и крышки К. Крышка на корпусе фиксируется штифтами и закрепляется на нем с помощью резьбовых деталей (болтов, шпилек, гаек). Редукторы бывают с осевой (продольной) и радиальной (поперечной) сборкой.

При осевой сборке разъем корпуса производят по плоскости, перпендикулярной осям валов (рис. 23.3, а). Такая конструкция более технологичная и жесткая (проще отливка, удобна механическая обработка). Недостатки: сложная сборка и осмотр внутренних частей.

При радиальной сборке разъем корпуса выполняют по плоскости, проходящей через оси валов (рис. 23.3, б), что облегчает сборку, разборку и осмотр внутренних полостей. Недостатки: изготовление корпуса сложнее, неодинаковая жесткость (асимметрия корпуса), сложнее герметизация (уплотнение по фигурному стыку).

Применение: осевую сборку применяют для создания прочных и легких конструкций в авиации, ракетостроении, на транспорте. Однако это вызывает некоторые эксплуатационные неудобства. Радиальную используют, если масса не играет существенной роли и допускается повышенная стоимость изготовления, ради удобства сборки и эксплуатации. Такие конструкции получили наибольшее распространение в общем машиностроении.

Корпуса(картеры) редукторов должны быть прочными и жесткими. Их отливают из серого чугуна, а для червячных редукторов – также из алюминиевых сплавов. Для удобства сборки корпуса редукторов выполняют разъемными (рис. 23.5).

Опорами валов редукторов, как правило, являются подшипники качения.

В редукторах с большим ресурсом работы предусматривается непрерывная смазка обычно жидким смазочным материалом. Для этого часть колеса погружают в масло (картерное смазывание) или подают его с помощью струи (струйное смазывание). Для подачи масла используется гидравлическая система. Смазывание подшипников часто осуществляется разбрызгиванием масла зубчатыми колесами.

При необходимости малого количества жидкого или пластичного смазочного материала (малый ресурс, малые скорости и нагрузки) он подается периодически с помощью масленок или ручного шприца. Иногда используют ресурсную смазку – один раз за весь ресурс (например, на ракетах).

Смазка зубчатых или червячных передач редукторов в большинстве случаев осуществляется окунанием, а подшипников – разбрызгиванием или консистентной смазкой. В корпус редуктора заливают масло из расчета 0,4¸0,7 л на 1 кВт передаваемой мощности, при этом колесо или червяк должны погружаться в масло на глубину не менее, чем высота зуба или витка.

Допускается погружать в масляную ванну тихоходные колеса многоступенчатых редукторов на глубину до 1/3 радиуса колеса .

Для защиты подшипников от попадания пыли, грязи и различных абразивных частиц, а также для предупреждения утечки смазки из корпуса редуктора применяют уплотнения подшипниковых узлов.

Билет 76) Основные понятия о соединениях

В механизмах отдельные детали для выполнения своих функций определенным образом соединяются между собой, образуя подвижные и неподвижные соединения (рис. 24.1). Подвижные соединения, например соединение вала с корпусом, зацепление зубчатых колес, шарниры и т.п., допускают взаимное движение одной детали относительно другой. Таким образом, подвижные соединения образуют кинематические пары. Неподвижные соединения не допускают взаимного перемещения сопрягаемых деталей. В машиностроении термин «соединения» относят только к неподвижным соединениям.

По признаку разъемности соединения подразделяются на разъемные и неразъемные.

Разъемные соединения – такие, которые допускают сборку и разборку без повреждения материала деталей. К этому виду соединений относятся резьбовые, шпоночные, шлицевые, штифтовые, профильные и клеммовые.

Неразъемные соединения – такие, которые невозможно разобрать без разрушения деталей. К ним относятся заклепочные, сварные, паяные, клеевые и соединения с натягом (прессовые).

Соединения являются ответственным элементом конструкций механизмов. Часто причиной отказов и разрушений механизмов является низкое качество соединений.

Предельное состояние соединения, когда становится возможной потеря его работоспособности, называется нагрузочной способностью.

Основным критерием работоспособности и расчета соединений является прочность.

При проектировании необходимо стремиться к тому, чтобы соединение было равнопрочным с соединяемыми элементами.Наличие соединения, которое обладает прочностью, составляющей, например, 0,8 от прочности самих деталей, свидетельствует о том, что 20% нагрузочной способности этих деталей или соответствующая часть металла конструкции не используется.

Желательно, чтобы соединение не искажало форму изделия, не вносило дополнительных элементов в его конструкцию и т.п. Например, соединение труб болтами требует образования фланцев, сверления отверстий под болты, установку самих болтов с гайками и шайбами. Соединение труб сваркой встык не требует никаких дополнительных элементов. Оно в наибольшей степени приближает составное изделие к целому. С этих позиций соединение болтами может быть оправдано только разъемностью.

Источник

Кинематический расчёт передачи.

1.Определение приближённого значения общего передаточного числа и разбивка его по ступеням , где К-число ступеней передачи.

Индекс «mr» означает, что передача выполняется от шестерни z_m к колесу z_r.

Для цилиндрических зубчатых передач коэффициент С_mr принимают:

— из условия минимума габаритов для развёрнутой схемы (К=2) С₁₂=1,2; (К=3) С₁₂=1,3; С =1. Передаточное число последней ступени (К=2) ; (К=3)

для соосных двухступенчатых редукторов .

— из условия минимума инерционности у быстроходных реверсивных приводов (К=2) С₁₂=0,6-0,95; (К=3) С₁₂=0,5-0,8, С =0,9-0,95.

Если на выходе стоит передача винт-гайка, то

, где v-скорость; n_вых — частота вращения вала на выходе, равная частоте вращения винта (гайки).

2. Выбор числа зубьев каждого колеса в паре:

— суммарное число зубьев для колёс с m>1 и однородной структурой z_Σ=z₁+z₂=80-90, для мелкомодульных m

4. Определение частоты вращения каждого вала:

n₂=n₁/u₁₂, .

Источник

Кинематический расчёт многоступенчатых передач.

Многоступенчатая передача с неподвижными осями зубчатых колёс состоит из ряда зубчатых пар, связанных в единую кинематическую цепь. Каждую зубчатую пару называют ступенью передачи. Задача кинематического расчёта многоступенчатой передачи состоит в том, чтобы определить передаточное отношение от ведущего вала к ведомому и направление вращения ведомого вала по заданному направлению вращения ведущего.

Пусть требуется выполнить кинематический расчёт четырёхступенчатой передачи (рис. 11.7). Ведущим валом, получающим движение от двигателя, служит вал с зубчатым колесом Z₁. Зубчатое колесо Z₇, связанное с последним ведомым валом, имеет в нашем примере внутренний зубчатый венец и образуется с колесом Z₆ зубчатую пару внутреннего зацепления. Зубчатое колесо Z₆ участвует в двух зубчатых парах. Известны числа зубьев зубчатых колёс.

Определяем передаточное отношение i₁₇ = ω₁/ω₇ (где ω₁ и ω₇ — угловая скорость ведущего и ведомого валов), а также знак передаточного отношения.

Для того чтобы вывести формулу для определения передаточного отношения многоступенчатой передачи, его разбивают на сомножители по числу ступеней и заменяют отношения угловых скоростей зубчатых колёс на каждой ступени соответствующими обратными отношениями чисел зубьев. Для плоских передач можно учитывать знак передаточного отношения на каждой ступени.

Передаточному отношению тех ступеней, где применяется внешнее зацепление, приписывается знак “минус” (так как при этом изменяется направление вращения ведомого вала), в случае внутреннего зацепления – знак “плюс”.

Для схемы, предоставленной на рис.11.7, передаточное отношение разбивается на четыре сомножителя:

Отношения угловых скоростей заменяются обратными отношениями чисел зубьев с учётом знаков передаточного отношения:

Здесь Z₁ — Z₇ — числа зубьев зубчатых колёс. После подстановок получаем:

ֹ

Передаточное отношение рассматриваемой четырёхступенчатой передачи имеет знак «минус», следовательно, ведущий и ведомый валы вращаются в разные стороны. Зубчатое колесо Z₆ не повлияло на числовое значение передаточное отношение, но изменило его знак. Такие зубчатые колёса называют паразитными колёсами. Их применяют для изменения направления вращения и для передачи движения между далеко отстоящими валами.

Планетарные зубчатые механизмы отличаются от других зубчатых механизмов тем, что имеют зубчатые колёса с подвижными осями вращения. Планетарный механизм с одной степенью свободы называются планетарной передачей. Планетарный механизм с двумя степенями свободы называется дифференциальным механизмом.

При кинематическом расчёте планетарных механизмов применяется уравнение связи угловых скоростей (формула Виллиса), составленное для механизмов с двумя степенями свободы, частными случаями которых являются механизмы с одной степенью свободы (планетарные передачи). Вследствие этого кинематические схемы тех и других планетарных механизмов требуется рассматривать параллельно.

На рис. 12.1 и 12.2 представлены кинематические схемы двух планетарных механизмов, различающихся числом степеней свободы.

Зубчатые колёса а и в, имеющие общую неподвижную ось вращения, называются центральными зубчатыми колёсами, а зубчатое колесо S с подвижной осью вращения – сателлитом. Звено h, на котором размещены подшипники сателлита, именуется водилом. Ось вращения водила совпадает с общей осью центральных зубчатых колёс. Водило и центральные зубчатые колёса являются основными звеньями планетарного механизма.

Механизм, кинематическая схема которого представлена на рис.12.1, имеет две степени свободы. Два любых центральных звена этого механизма можно рассматривать как ведущие звенья. Например, ведущими звеньями могут быть колесо а и водило h, при этом колесо в становится ведомым звеном.

На рис.12.2 приведена кинематическая схема планетарной передачи. Она отличается от предыдущей схемы тем, что одно из центральных зубчатых колёс (колесо в) остановлено и закреплено на стойке, вследствие чего степеней свободы механизма уменьшилось на единицу. Этот механизм можно применять в качестве понижающей передачи (если передавать движение от колеса а к водилу h) или в качестве повышающей передачи (при передачи движения от водила на колесо а).

Из механизма с двумя степенями свободы можно получить вторую планетарную передачу, если остановить и закрепить на стойке зубчатое колесо а. При этом подвижными звеньями останутся колёсо в и водило h, каждое из которых можно рассматривать как ведущее звено.

Из любого пятизвенного планетарного механизма с двумя степенями свободы образуется две планетарные передачи путём поочередной остановки одного из центральных зубчатых колёс.

На рис. 12.3 представлены кинематические схемы пятизвенных планетарных механизмов с двумя степенями свободы, сателлиты которых имеют два зубчатых венца. Они отличаются друг от друга различными комбинациями способов зацепления центральных зубчатых колёс и зубчатых колёс сателлита (внешнее зацепление, внутреннее зацепление).

a – с двумя внешними зацеплениями;

б – с одним внешним и одним внутренним зацеплением;

в – с двумя внутренними зацеплениями.

На рис. 12.4 изображены кинематические схемы четырёхзвенных планетарных передач, полученных посредством остановки и закрепления центрального колеса в. Путём закрепления колеса а также можно образовать три планетарных передачи.

На практике часто применяют планетарные механизмы, в которых зубчатые венцы S и t совмещены. В этом случае упрощается изготовление и сборка механизма. При совмещении зубчатых венцов сателлитов в планетарной передаче с одним внешним и одним внутренним зацеплением (рис. 12.4, б) получаем планетарную передачу, схему которой представлена на рис. 12.2.

В связи с выбором ведущего звена в планетарной передачи необходимо коснуться вопроса о потерях на трение в планетарных механизмах, которых выходит за рамки структурного и кинематического анализа, но имеет важное практическое значение.

При назначении ведущего звена для планетарной передачи с двумя внешними или двумя внутренними зацеплениями (рис.12.4, а, в) необходимо учитывать, что здесь в случае передачи движения от центрального колеса к водилу возможно резкое падение коэффициента полезного действие. При малой разности чисел зубьев зубчатых колёс S и t сателлита и в случае их совмещения происходит самоторможение, механизм не проворачивается. Ввиду этого ведущим звеном в упомянутых передачах служит, как правило, водило.

Источник