Каков момент силы трения лестницы

рис.1

рис.2
Прежде всего отметим, что лестница, прислоненная к вертикальной стенке, вообще не может находиться в равновесии, если нет трения о пол — она обязательно соскользнет по стенке. Более того, верхний конец лестницы при таком соскальзывании обязательно отделится от стенки раньше, чем лестница окажется на полу. Невозможность равновесия у вертикальной стенки на гладком полу очевидна из рис. 1: нормальная сила реакции стенки $\vec_<2>$ должна быть отлична от нуля так как иначе не будет уравновешен момент силы тяжести $m \vec$ относительно точки А; но сама сила $\vec_<2>$ может быть уравновешена только горизонтально направленной силой трения о пол.

А вот равновесие у наклонной шероховатой стенки возможно и на идеально гладком полу. На рис. 2 изображены силы, действующие на лестницу. Поскольку силы $m \vec$ и $\vec_<1>$ направлены вертикально, то в равновесии горизонтальные составляющие силы $\vec_<2>$ и $\vec_<тр>$ должны быть равны:

$N_ <2>\cos \beta = F_ <тр>\sin \beta$. (1)

Сила трения покоя $\vec_<тр>$ максимальна на пороге проскальзывания, когда ее значение равно $\mu N_<2>$. Из формулы (1) в этом случае находим

Формула (2) дает минимальное значение коэффициента трения $\mu$, при котором возможно равновесие у наклонной стенки с углом наклона $\beta$ в отсутствие трения о пол. При этом лестница как бы цепляется за шероховатую стенку, а другим концом давит на гладкий пол.

Обратим внимание на то, что условие равновесия лестницы не зависит ни от того, насколько наклонена сама лестница, ни от того, в каком месте приложена сила тяжести $m \vec$ и каково ее значение. Это значит, что лестница будет в равновесии и в том случае, если на ней в любом месте стоит человек.

Отметим, наконец, что условие (2) совпадает с выражением для предельного коэффициента трения, при котором возможно равновесие небольшого бруска, положенного на наклонную стенку.
Ответ: $\mu = ctg \beta$.

Источник

Каков момент силы трения лестницы

Максимальный угол наклона к вертикали, под которым может стоять лестница массой m, прислонённая к вертикальной гладкой стене и опирающаяся на горизонтальный шероховатый пол, равен Коэффициент трения между ножками лестницы и полом равен Лестницу установили, наклонив её именно под углом

Из приведённого ниже списка выберите два правильных утверждения.

1) Модуль силы реакции со стороны стены больше модуля силы трения между ножками лестницы и полом.

2) Модуль силы трения между лестницей и полом равен произведению коэффициента трения на модуль силы реакции со стороны стены.

3) Модуль силы трения между лестницей и полом равен произведению коэффициента трения на модуль силы тяжести.

4) Модуль силы тяжести меньше модуля силы реакции со стороны пола.

5) Момент силы трения относительно оси, проходящей через точку А, равен нулю.

На лестницу действуют силы, изображенные на рисунке.

1. Неверно. Так как лестница находится в равновесии, то В проекции на ось ОX:

2. Неверно. Сила трения равна

3. Верно. В проекции на ось OY: следовательно,

4. Неверно. См. пункт 3.

5. Верно. Линия действия силы трения проходит через точку А, поэтому M = 0.

Источник

Как определить момент сил трения?

Когда решают любые задачи по физике, в которых имеются движущиеся объекты, то всегда говорят о силах трения. Их либо учитывают, либо ими пренебрегают, но факт их присутствия ни у кого не вызывает сомнения. В данной статье рассмотрим, что такое момент сил трения, а также приведем проблемы, для устранения которых воспользуемся полученными знаниями.

Сила трения и ее природа

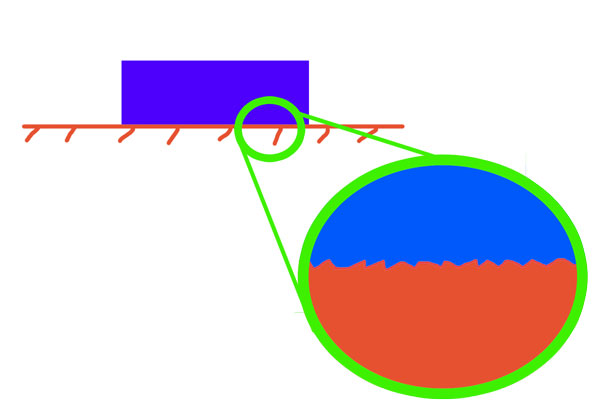
Каждый понимает, что если одно тело движется по поверхности другого совершенно любым способом (скользит, катится), то всегда существует некоторая сила, которая препятствует этому перемещению. Она называется динамической силой трения. Причина ее возникновения связана с тем фактом, что любые тела имеют микроскопические шероховатости на своих поверхностях. Когда соприкасаются два объекта, то их шероховатости начинают взаимодействовать друг с другом. Это взаимодействие носит как механический характер (пик попадает во впадину), так и происходит на уровне атомов (дипольные притяжения, ван-дер-ваальсовые и другие).

Когда соприкасаемые тела находятся в покое, то, чтобы привести их в движение относительно друг друга, необходимо приложить усилие, которое больше такового для поддержания скольжения этих тел друг по другу с постоянной скоростью. Поэтому помимо динамической также рассматривают статическую силу трения.

Свойства силы трения и формулы для ее вычисления

В школьном курсе физики говорится, что впервые законы трения изложил французский физик Гийом Амонтон в XVII веке. На самом деле это явление стал изучать еще в конце XV века Леонардо да Винчи, рассматривая движущийся предмет по гладкой поверхности.

Свойства трения могут быть кратко изложены следующим образом:

• сила трения всегда действует против направления перемещения тела;
• ее величина прямо пропорциональна реакции опоры;
• она не зависит от площади контакта;
• она не зависит от скорости перемещения (для небольших скоростей).

Эти особенности рассматриваемого явления позволяют ввести следующую математическую формулу для силы трения:

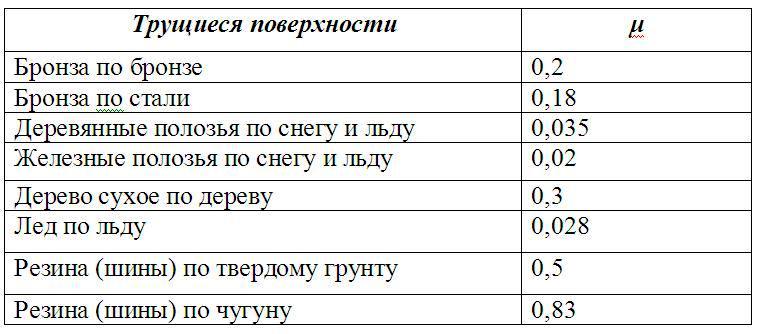
F = μ*N, где N — реакция опоры, μ — коэффициент пропорциональности.

Значение коэффициента μ зависит исключительно от свойств поверхностей, которые трутся друг о друга. Таблица значений для некоторых поверхностей приведена ниже.

Для трения покоя формула используется та же самая, что приведена выше, однако значения коэффициентов μ для тех же поверхностей будут совершенно иные (они больше по величине, чем для скольжения).

Особый случай представляет трение качения, когда одно тело катится (не скользит) по поверхности другого. Для силы в этом случае применяют формулу:

Здесь R — радиус колеса, f- коэффициент качения, который согласно формуле имеет размерность длины, что его отличает от безразмерного μ.

Момент силы

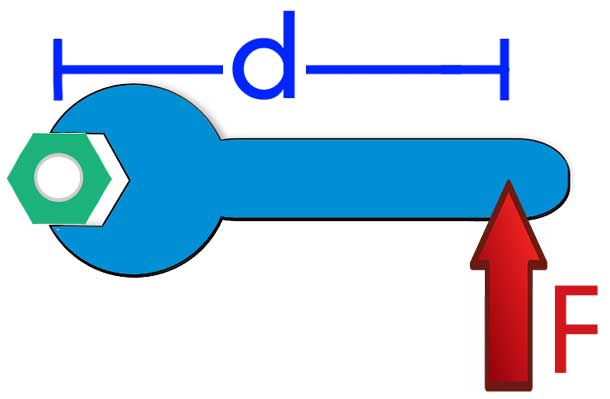
Перед тем как отвечать на вопрос, как определить момент сил трения, необходимо рассмотреть само физическое понятие. Под моментом силы M понимают физическую величину, которая определяется как произведение плеча на значение силы F, приложенной к нему. Ниже приведен рисунок.

Здесь мы видим, что приложение F к плечу d, которое равно длине гаечного ключа, создает крутящий момент, приводящий к откручиванию зеленой гайки.

Таким образом, для момента силы справедлива формула:

Заметим, что природа силы F не имеет никакого значения: она может быть электрической, гравитационной или вызванной трением. То есть определение момента силы трения будет тем же самым, что приведено в начале пункта, и записанная формула для M остается справедливой.

Когда появляется момент сил, вызванный трением?

Эта ситуация возникает, когда выполняются три главных условия:

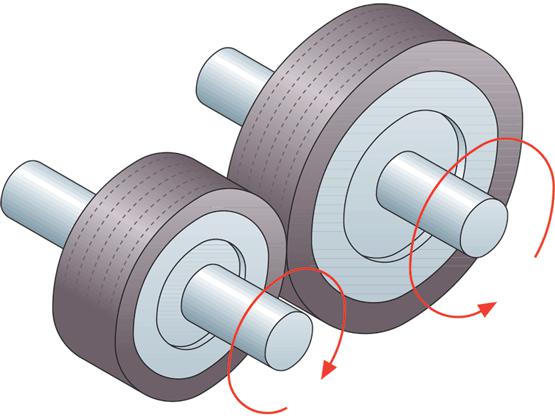
• Во-первых, должна иметь место вращающаяся система вокруг некоторой оси. Например, это может быть колесо, движущееся по асфальту, или крутящаяся на оси горизонтально расположенная музыкальная пластинка патефона.
• Во-вторых, должно существовать трение между вращающейся системой и некоторой средой. В примерах выше: на колесо действует трение качения при его взаимодействии с поверхностью асфальта; если положить музыкальную пластинку на стол и раскрутить ее, то она будет испытывать трение скольжения о поверхность стола.
• В-третьих, возникающая сила трения должна действовать не на ось вращения, а на крутящиеся элементы системы. Если сила имеет центральный характер, то есть действует на ось, то плечо равно нулю, поэтому она не будет создавать момента.

Как найти момент силы трения?

Чтобы решить эту задачу, необходимо сначала определить, на какие вращающиеся элементы действует сила трения. Затем следует найти расстояние от этих элементов до оси вращения и определить, чему равна сила трения, действующая на каждый элемент. После этого необходимо выполнить умножение расстояний r_i на соответствующие величины F_i и сложить полученные результаты. В итоге суммарный момент сил трения вращения вычисляется по формуле:

Здесь n — количество сил трения, возникающих в системе вращения.

Любопытно отметить, что хотя M — это величина векторная, поэтому при сложении моментов в скалярной форме следует учитывать ее направление. Трение всегда действует против направления вращения, поэтому каждый момент M_i=r_i*F_i будет иметь один и тот же знак.

Далее решим две задачи, где используем рассмотренные формулы.

Вращение диска болгарки

Известно, что когда диск болгарки радиусом 5 см режет металл, то он вращается с постоянной скоростью. Необходимо определить, какой момент сил создает электромотор прибора, если сила трения о металл диска равна 0,5 кН.

Поскольку диск вращается с постоянной скоростью, то сумма всех моментов сил, которые на него действуют, равна нулю. В данном случае мы имеем всего 2 момента: от электромотора и от силы трения. Поскольку они действуют в разных направлениях, то можно записать формулу:

Поскольку трение действует только в точке соприкосновения диска болгарки с металлом, то есть на расстоянии r от оси вращения, то ее момент силы равен:

Поскольку электромотор создает такой же по модулю момент, получаем ответ: 25 Н*м.

Качение деревянного диска

Имеется диск из дерева, его радиус r равен 0,5 метра. Этот диск начинают катить по деревянной поверхности. Необходимо рассчитать, какое расстояние способен он преодолеть, если начальная скорость вращения его ω составляла 5 рад/с.

Кинетическая энергия вращающегося тела равна:

Здесь I — момент инерции. Сила трения качения будет приводить к замедлению движения диска. Работу, совершаемую ей, можно вычислить по следующей формуле:

Здесь θ — угол в радианах, на который сможет повернуться диск в процессе своего движения. Тело будет катиться до тех пор, пока вся его кинетическая энергия не расходуется на работу трения, то есть можно приравнять выписанные формулы:

Момент инерции диска I равен m*r 2 /2. Чтобы вычислить момент M силы трения F, следует заметить, что она действует вдоль края диска в точке его соприкосновения с деревянной поверхностью, то есть M = r*F. В свою очередь F = f*mg/r (сила реакции опоры N равна весу диска mg). Подставляя все эти формулы в последнее равенство, получим:

Поскольку пройденное диском расстояние L связано с углом θ выражением L=r*θ, то получаем конечное равенство:

Значение f можно посмотреть в таблице для коэффициентов трения качения. Для пары дерево-дерево он равен 1,5*10 -3 м. Подставляем все величины, получаем:

Для подтверждения правильности полученной конечной формулы можно проверить, что получаются единицы измерения длины.

Источник

Определить, при каком коэффициенте трения между основанием лестницы и асфальтом лестница не упадёт

Лестницу длиной 2,50 м и массой 30 кг прислонили к стене дома. Она составляет со стеной угол 60°. Определите, при каком коэффициенте трения между основанием лестницы и асфальтом лестница не упадёт
Желательно подробное решение

Комментарий модератора

Правила форума, пункт 4.3. Создавайте темы с осмысленными и понятными названиями — это серьезно повышает шансы, что на ваш вопрос ответят. Правила форума, пункт 4.7. Как можно более полно описывайте суть проблемы или вопроса, что было сделано для ее решения и какие результаты получены.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

При каком минимальном коэффициенте трения между столом и клином последний будет оставаться в покое?
Помогите решить) Шайба массой m соскальзывает по гладкой наклонной поверхности клина массы 2m.

При каком наименьшем коэффициенте трения между столом и большим кубиком последний будет оставаться неподвижным?
Три кубика имеют равные массы и могут скользить вдоль друг друга без трения. Два кубика связаны.

При каком условии начнется движение ,если коэффициент трения между телом м1 и наклонной плоскостью равен к
Тело массы м1 находится на горизонтальной плоскости и пригодится в движение грузом массы.

Определить, при каком значении коэффициента трения катушка начинает проскальзывать
Проволока из сплава хромель-алюмель намотана на деревянный цилиндр массы m, лежащий на параллельных.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

При каком значении коэффициента трения катушка начинает проскальзывать
Проволока из сплава хромель-алюминий намотана на деревянный цилиндр массы m, лежащий на.

Определить, при каком х расстояние между f1 (x) и f2 (x) максимально
Помогите пожалуйста с двумя задачами: 1) Значения функции f1(х)=3+sqr(sin(x/2)) и.

На каком расстоянии S от наклонной плоскости коробок упадет?
Коробок после удара в точке A скользит вверх по наклонной плоскости с начальной скоростью V0 = 5.

На каком расстоянии от конца желоба шарик упадет на пол?
Здравствуйте!Помогите пожалуйста решить задачу по физике? По кривому желобу, установленному на.

Определить силу трения между образующей и плоскостью, по которой катится конус.
круглый стальной конус (высота 10 см и радиус основания 4 см) катится без скольжения по.

Источник