- Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену
- Условие задачи:
- Решение задачи:
- Ответ: 1,22 рад.
- Как решать задачи про лестницу
- Как решать задачи про лестницу
- Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до N-й ступеньки?
- Как решать задачи про лестницу
Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену
Условие задачи:
Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену, а нижним – в пол под углом 60° к горизонту. На лестнице на расстоянии 1 м от её верхнего конца стоит человек массой 60 кг. Под каким углом к горизонту направлена сила, с которой пол действует на нижний конец лестницы?
Задача №3.1.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
\(m=15\) кг, \(L=3\) м, \(\alpha=60^\circ\), \(l=1\) м, \(M=60\) кг, \(\beta – ?\)
Решение задачи:
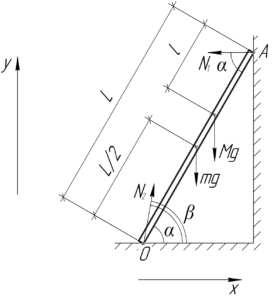
\[\left\< \begin
mg \cdot \frac
\end
Поделим равенства (1) и (2) друг на друга:
Из равенства (3) выразим реакцию \(N_1\):
Полученное подставим в (4), тогда:
Окончательная формула примет вид:
Посчитаем численное значение искомого угла \(\beta\):
\[\beta = arctg\left( <\frac<<\left( <15 + 60>\right) \cdot 2 \cdot 3 \cdot tg60^\circ >> <<15 \cdot 3 + 2 \cdot 60 \cdot \left( <3 – 1>\right)>>> \right) = 70^\circ = 1,22\;рад\]
Ответ: 1,22 рад.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Как решать задачи про лестницу
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке. Таким образом, задача сводится к нахождению гипотенузы прямоугольного треугольника; обозначим её за По теореме Пифагора:
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
Пусть длина искомой стороны равна Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке, тогда
— катет получившегося прямоугольного треугольника. По теореме Пифагора:
Следовательно, длина искомой стороны равна 9.
Источник
Как решать задачи про лестницу
Когда колено болит и хромаешь, поневоле начинаешь считать ступеньки.
Давайте представим себе, что за один шаг мы можем подняться либо на одну, либо на две ступеньки.
Всего ступенек на лестнице N .
Сколько существует способов подняться по лестнице?
Для решения не нужно ничего, кроме элементарной логики.
Очевидно, что на первую ступеньку можно подняться только одним способом, сделав короткий шаг, а на вторую — двумя, либо два коротких шага, либо один длинный.
Как насчёт третьей ступеньки?
По условию, существует только два варианта попасть на неё — либо мы сделали короткий одиночный шаг со ступеньки 2, либо это был двойной шаг со ступеньки 1.
Мы знаем, что у нас есть только один способ достичь первой ступеньки, и два способа достичь второй. Так как третьей ступеньки мы можем достичь со второй или с первой, сложив эти количества, видим, что подняться на третью ступеньку имеется 3 способа (1-1-1, 1-2, 2-1).
Та же логика применяется и дальше. Попасть на четвёртую ступеньку можно со второй (куда было два способа добраться) или с третьей (куда можно влезть тремя способами). Получается пять способов для ступени 4.
Если кто ещё не догадался, мы встретились с миллион первым применением чисел Фибоначчи, а для них имеется явная формула вычисления N-го члена ряда, известная как формула Бине.
Таким образом, проблема решается со сложностью O(1) и ничего перебирать не надо.
Между прочим, подобную задачу часто предлагали решить соискателям при трудоустройстве программистом в компанию Google 🙂
30.05.2018, 12:10; рейтинг: 1101
Источник
Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до N-й ступеньки?
Начало здесь простое. Вы стоите на лестничном марше и хотите подняться на первую ступеньку — № 1. Для этого надо сделать всего одно действие — подняться на одну ступеньку вверх. Теперь давайте рассмотрим вторую ступеньку, то есть N = 2. Чтобы подняться на неё, имеются два варианта. Вы можете сделать два шага — по одной ступеньке за раз или сразу подняться на вторую ступеньку.
Это практически вся информация, которая нужна вам для решения этой задачи. Чтобы понять, почему, представьте, что вашей целью является ступенька № 3. Впервые в этой ситуации вы не можете попасть на неё одним движением. здесь потребуется комбинация шагов. Существует только два способа попадания на ступеньку № 3: либо в виде короткого одиночного шага (со ступеньки № 2), либо двойного шага (со ступеньки № 1). Мы уже знаем, что для подъема на ступеньку № 1 имеется лишь один вариант. Мы также знаем, что есть всего два способа подняться на ступеньку № 2. Сложите эти варианты (1 + 2 = 3), и вы получите число способов, позволяющих подняться на ступеньку № 3.
Та же самая логика применяется для подъема на каждую следующую ступеньку. Существует два способа, чтобы подняться на ступеньку № 4 — со ступеньки № 2 или со ступеньки № 3. Добавьте число способов подъема на ступеньку № 2 (2) к числу способов, позволяющих оказаться на ступеньке № 3 (3). Это даёт 5 вариантов — число способов, позволяющих оказаться на ступеньке № 4.
Легко продолжить эту серию и дальше. С увеличением числа ступенек число способов подниматься по ним нарастает, как снежный ком, что можно представить в следующем виде:
Это просто число Фибоначчи под номером N. Леонардо Фибоначчи, также известный как Леонардо Пизанский, был самым влиятельным итальянским математиком в Средние века. Именно Фибоначчи понял невероятное превосходство арабскo-индийской позиционной системы исчисления по сравнению с римским обозначением цифр, которое все ещё использовалось в средневековой Европе. При помощи арабско-индийской системы умножение и деление можно было свести к алгоритму (еще одно арабское слово). При применении римских чисел эти операции на практике выполнять было сложно. Торговцам приходилось приглашать экспертов и дорого им платить за вычисления, которые те осуществляли при помощи абаков. В 1202 году Фибоначчи написал Liber abaci — руководство по использованию абака, в котором он расхваливал арабские числа своим читателям, которые были, скорее всего, настроены к ним скептически. В этой книге также описывается и та серия чисел, которую мы теперь называем по его фамилии. Однако её изобрел не Фибоначчи. Эта последовательность была известна еще индийским ученым, жившим в VI веке.
Напишите 1, а затем добавьте еще 1 рядом. Сложите их и получите сумму (2), которая затем добавляется к формируемой последовательности:
Для получения каждого нового члена лишь складывайте последние два числа в ряду/ Серия примет следующий вид.
1 1 2 3 5 8 13 21 34 55 89 144…
Поклонники теории заговоров отыскивают серии Фибоначчи в самых неожиданных местах. Хотите перевести расстояние из миль в километры? Воспользуйтесь соседними числами Фибоначчи (55 миль в час = 89 километров в час). В следующий раз, когда у вас окажется свободное время, посчитайте небольшие дольки, из которых состоит кожура ананаса, и вы обнаружите, что они образуют два накладывающихся друг на друга набора спиралей, идущих в противоположных направлениях. В одной из них восемь долей, в другой тринадцать. Оба этих числа относятся к серии Фибоначчи. Аналогичные закономерности можно увидеть в сосновых шишках, подсолнухах и артишоках. Случайность? Вряд ли, если учесть тот факт, что последовательность Фибoначчи проявила себя и в Коде Да Винчи (в виде комбинации для вскрытия сейфа), и в этом вопросе на собеседовании, который задают в компании, стремящейся к информационному доминированию во всем мире (Google, если вы не поняли).
Источник
Как решать задачи про лестницу
Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен:
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Задача сводится к нахождению гипотенузы прямоугольного треугольника, по теореме Пифагора она равна:
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Это задание ещё не решено, приводим решение прототипа.
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен:
Источник
