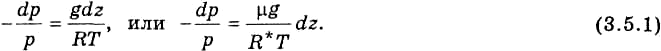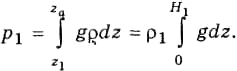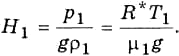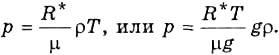Как определить барическую ступень

Барометрическая ступень

Барометри́ческая ступе́нь (бари́ческая ступе́нь) — величина, определяющая изменение высоты в зависимости от изменения атмосферного давления. Применяется при барометрическом нивелировании и при пересчёте показаний статоскопа в разность высот.

Зависит от давления и температуры воздуха.

Наглядный смысл барометрической ступени — высота, на которую надо подняться, чтобы давление понизилось на 1 гПа.

Содержание

Применение

, где

• — изменение высоты , метры
• — изменение давления, кПа
• — значение барометрической ступени, м/кПа
• — температура, градусы Цельсия
• — давление, кПа в месте измерения

Формула практически точна при небольших (десятки метров) изменениях высоты.

Вычисление барометрической ступени

(смысл и размерности величин см выше).

Таблица величины барометрической ступени (м/кПа) для некоторых значений давления и температуры:

Давление, кПа	Температура, °C
	−40	−20	0	20	40
100	67	74	80	86	93
50	134	147	160	173	186
10	672	736	800	864	928

Пример

При переносе барометра с уровня моря на холм давление уменьшилось на 2 мм.рт.ст. Температура комнатная. Какова высота холма?

1 мм.рт.ст = 101,325/760 мм = 0.13332 кПа.

Положим, что давление на уровне моря равно стандартному:

Δp = — 2 мм.рт.ст. = — 2 • 0,13332 кПа/мм.рт.ст = — 0,26664 кПа

Из формулы: Q = 84.7 м/кПа (или 11.29 метра на 1 мм.рт.ст).

Изменение высоты (высота холма) Δh = 84.7 • 0,26664 = 22,59 ≈ 22,6 метра

Разницу можно вычислить также по барометрической формуле: Δh = 18400*(1 + a*t)*lg (p1 / p2) (в метрах), где t — средняя температура слоя воздуха между точками измерения в градусах, a — температурный коэффициент объёмного расширения воздуха 0.00366. Или 18400*(1 + 0.00366*20)*lg (760 / (760+2 мм)) = 22.54 метра.

См. также

Литература и ссылки

• Приходько М. Г. Справочник инженера-синоптика. — Л. : Гидрометеоиздат, 1986. — С. 16. — 328 с.
• Хромов С. П. Метеорология и климатология для географических факультетов. — Л. : Гидрометеорологическое изд-во, 1964. — С. 69. — 500 с.
• статья «Барическая ступень» в БСЭ

Wikimedia Foundation . 2010 .

Смотреть что такое «Барометрическая ступень» в других словарях:

Барометрическая ступень — то же, что Барическая ступень … Большая советская энциклопедия

Барометрическая формула — Барометрическая формула зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения… … Википедия

Барическая ступень — барометрическая ступень, разность высот двух точек на одной вертикали, соответствующая разности атмосферного давления в 1 мбар между этими точками (1 мбар = 100 н/м2). Б. с. тем больше, чем ниже давление. Поэтому с высотой она… … Большая советская энциклопедия

барическая ступень высоты — барическая ступень Ндп. барометрическая ступень Расстояние по вертикали, соответствующее изменению атмосферного давления на единицу. [ГОСТ 22268 76] Недопустимые, нерекомендуемые барометрическая ступень Тематики геодезия Обобщающие термины… … Справочник технического переводчика

Барическая ступень высоты — 99. Барическая ступень высоты Барическая ступень Ндп. Барометрическая ступень D. Barometrische Höhenstufe E. Barometric height increment F. Échelon de pression d altitude Расстояние по вертикали, соответствующее изменению атмосферного давления на … Словарь-справочник терминов нормативно-технической документации

ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации

Источник

Эта статья перенесена сюда!

Давление атмосферы непрерывно изменяется по вертикали и в горизонтальном направлении. По мере увеличения высоты места давление понижается, так как уменьшается столб воздуха и его плотность. Высота, на которую надо подняться или опуститься, чтобы давление изменилось на 1 гПа, называется барической (барометрической) ступенью. У земной поверхности при давлении 1000 гПа и температуре 0°С она равна 8 м/гПа. С ростом температуры и увеличением высоты над уровнем моря она возрастает, т. е. она прямо пропорциональна температуре и обратно пропорциональна давлению. Величина, обратная барической ступени, – вертикальный барический градиент, т. е. изменение давления при поднятии или опускании на 100 метров . При температуре 0°С и давлении 1000 мб он равен 12,5 гПа.

Давление воздуха, гПа (мм. рт. ст.).

Пространственное распределение атмосферного давления называют барическим полем. Распределение давления по вертикали изображается с помощью изобарических поверхностей – воображаемых поверхностей в атмосфере, соединяющих точки с одинаковым атмосферным давлением. На их расположение в пространстве большое влияние оказывает температура. При одинаковом давлении у земной поверхности одни и те же изобарические поверхности в теплом воздухе (например, на экваторе) лежат выше, чем в холодном (например, на полюсах). Это объясняется тем, что в холодном и более плотном воздухе давление с высотой уменьшается быстрее, т. е. барическая ступень там меньше, чем в теплом воздухе. Рельеф изобарических поверхностей в тропосфере показывается на специальных картах с помощью изогипс – линий равной высоты над уровнем моря, на которых лежит в данном месте та или иная изобарическая поверхность. Такие карты носят название карт абсолютной барической топографии (AT). В синоптической практике принято анализировать изобарические поверхности 850, 700, 500, 300 и 200 мб, лежащие соответственно на высотах около 1,5, 3, 5, 7 и 9 км .

Изобарические поверхности в областях тепла и холода в разрезе

Изменение давления на уровне моря показывается с помощью изобар – линий на карте, соединяющих точки с одинаковым приземным атмосферным давлением, обязательно приведенным к уровню моря. Принято показывать изобары, кратные 5 мб, например 995, 1000, 1005, 1010 мб и т. д. Изобары, подобно горизонталям на топографических картах, могут иметь разнообразную конфигурацию. То же можно сказать и об изогипсах, которые, по сути дела, являются теми же горизонталями – линиями равных высот.

Изобары и изогипсы могут быть замкнутыми и незамкнутыми. Система замкнутых изобар с пониженным давлением в центре называется барическим минимумом или циклоном. Система замкнутых изобар с повышенным давлением в центре называется барическим максимумом или антициклоном. На высоте в циклонах изобарические поверхности, не касающиеся поверхности Земли, прогнуты вниз в виде воронок и образуют замкнутые понижения, а в антициклонах, наоборот, выгнуты вверх в виде замкнутых куполов. Кроме замкнутых барических систем, у Земли и в тропосфере выделяются незамкнутые системы: ложбины, гребни и седловины.

Изобарические поверхности в антициклоне (В) и циклоне (Н) в вертикальном разрезе и их проекции — изобары на плоскости

Ложбина – связанная с циклоном и вытянутая от его центра к периферии полоса пониженного давления, расположенная между двумя областями повышенного давления.

Гребень – связанная с антициклоном и вытянутая от его центра к периферии полоса повышенного давления, расположенная между двумя областями пониженного давления.

Седловина – участок барического поля между двумя циклонами и антициклонами, расположенными крест-накрест.

Барические системы (изобары в мб)

На высоте эти системы соответствуют своим названиям и на картах AT так и изображаются: ложбинами, гребнями и седловинами. Горизонтальные размеры барических систем изменяются от сотен до тысяч километров, их вертикальная протяженность достигает нескольких километров.

1. Любушкина С.Г. Общее землеведение : Учеб. пособие для студентов вузов, обучающихся по спец. «География» / С.Г. Любушкина, К.В. Пашканг, А.В. Чернов; Под ред. А.В. Чернова. — М. : Просвещение, 2004. — 288 с.

Источник

3.4. Барическая ступень

Для приближенной оценки высоты по известной разности давле­ний или, наоборот, для оценки давления по заданной разности вы­сот на практике удобно пользоваться понятием “барическая сту­пень”.

Барической ступенью называется такая высота, на которую нуж­но подняться с исходного уровня, чтобы давление понизилось на 1 гПа. Обозначим ее через Л. Единица барической ступени — м/гПа. Формулу для барической ступени легко получить, если воспользо­ваться следующими рассуждениями. При увеличении высоты на dz давление понижается на -dp. Для того чтобы давление уменьши­лось на 1 гПа, необходимо подняться на высоту

С учетом уравнения (3.2.5) эта формула принимает вид

Формула (3.4.2) показывает, что h зависит только от плотности воздуха (не считая зависимости от g, которое изменяется в узких пределах). Чем меньше плотность воздуха, тем больше барическая ступень, и наоборот.

Исследуем зависимость барической ступени от высоты (давле­ния) и температуры. С увеличением высоты плотность воздуха, как было показано в п. 3.3, уменьшается, если исключить из рассмотре­ния тонкий приземной слой, в котором плотность может и возрас­тать с высотой (при у > уд). Уменьшение плотности приводит к рос­ту барической ступени при увеличении высоты. Подставив в форму­лу (3.4.2) плотность р из уравнения (1.4.12), получим:

Если сравниваются барические ступени на одной и той же изоба­рической поверхности (р = const) в двух воздушных массах (теплой и холодной), то, согласно (3.4.3), барическая ступень в теплой массе (h_т) больше барической ступени в холодной массе (h_х), т. е. h_т > h_х. Чем меньше барическая ступень, тем быстрее падает с вы­сотой давление. Значения барической ступени при разных темпера­турах и давлениях приведены в табл. 3.1.

Таблица 3.1. Барическая ступень (м/гПа)

Температура, o С

3.5. Вертикальный масштаб атмосферы

Барометрические формулы широко используются, в частности, при изучении свойств верхних слоев атмосферы (термосферы и экзосферы) с помощью ИСЗ, космических кораблей и ракет. Отметим, что атмосфера и на больших высотах оказывает существенное влия­ние на летательные аппараты при их длительном пребывании в ней: под влиянием силы сопротивления происходит постепенное умень­шение полной механической энергии спутника и, следовательно, изменение элементов орбиты. Сила сопротивления и скорость изме­нения элементов орбиты спутника прямо пропорциональны плотно­сти воздуха на высоте полета. При облете Земли спутник проходит через слои атмосферы с различной плотностью. Для оценки влия­ния атмосферы на изменение элементов орбиты за полный оборот необходимо знать зависимость плотности воздуха от высоты. Выве­дем формулы для распределения давления и плотности воздуха по высоте в верхних слоях атмосферы, которые обобщают формулы п. 3.3. Необходимость такого обобщения диктуется тем, что в верх­них слоях атмосферы изменяется с высотой не только температура, но и молекулярная масса (состав воздуха). Ускорение свободного па­дения при изменении высоты в широких пределах также нельзя принимать за постоянную величину.

Если, как и в п. 3.3, в основном уравнении статики (3.2.4) плот­ность воздуха заменить по уравнению состояния (1.4.8), то полу­чим:

При последнем переходе R заменено на R*/μ. (здесь R* — универ­сальная газовая постоянная, μ — относительная молекулярная мас­са воздуха).

Одно из важнейших свойств уравнений заключается в том, что размерности их левой и правой части должны быть одинаковыми. Левая часть (3.5.1) безразмерная. Следовательно, и правая часть должна быть безразмерной. Однако множитель dz в правой части имеет размерность длины. Таким образом, приходим к заключению о том, что вошедшая в правую часть (3.5.1) величина

также имеет размерность длины; в этом можно убедиться и путем непосредственной проверки. Параметр Н, объединяющий три пере­менные величины (T, μ, g), называют высотой однородной атмосфе­ры или вертикальным масштабом атмосферы. После введения Н основное уравнение статики принимает следующий вид:

По своему физическому смыслу параметр Н совпадает с введен­ной в п. 3.2 высотой однородной атмосферы. Различие состоит в том, что в п. 3.2 в выражение для Н входила температура у земной поверхности, в то время как в формулу (3.5.2) входит температура на произвольной высоте. Но во всех случаях Н — это толщина та­кой однородной атмосферы, у которой давление и плотность на ее нижней границе равны давлению и плотности на том уровне в ре­альной атмосфере, для которого по формуле (3.5.2) рассчитан пара­метр Н. Чтобы убедиться в этом, достаточно обратиться к формуле (3.2.7). Пусть на каком-либо фиксированном уровне z₁ давление бу­дет p₁, плотность ρ₁ и температура Т₁. Тогда, согласно (3.2.7) и определению толщины H₁ однородной атмосферы, в которой (на всех высотах) плотность равна ρ₁( можем записать

Пренебрегая зависимостью g от z, получаем: p₁ = gρ₁H₁, т. е.

Эта формула совпадает с формулой (3.5.2), хотя получена она на основе представления об Н как о толщине однородной атмосферы.

Параметр Н можно ввести также и в уравнение состояния воз­духа:

Подчеркнем, что с введением параметра Н, объединяющего три переменные величины (T, μ, g), при получении барометрических формул отпадает необходимость раздельного учета изменения каж­дой из этих величин (в частности, g) с высотой. Формула (3.5.3) по­казывает, что изменение давления обусловливается распределением по высоте именно Н, а не каждой из трех переменных величин в от­дельности.

В общем случае Н является достаточно сложной функцией высо­ты; выше 95—100 км изменяются с высотой не только Т и g, но и μ. Если в некотором слое параметр Н считать постоянным (Н = const), то, интегрируя уравнение (3.5.3), получим барометрическую формулу для такого слоя в виде

где z_π — высота нижней границы слоя, р_π — давление воздуха на этой границе. Именно в таком виде чаще всего используется баро­метрическая формула при решении задач о влиянии атмосферы на изменение элементов орбиты, а также на время существования ИСЗ и других летательных аппаратов. В качестве нижней границы z_π в этих случаях берется высота перигея спутника.

Если уравнение состояния (3.5.4) записать для уровня z_π:

то после деления (3.5.4) на (3.5.6) с учетом формулы (3.5.5), получа­ем формулу для плотности воздуха в слое с Н = const:

Обычно изменением g с высотой пренебрегают, полагая в послед­ней формуле g_π/g ≈ 1.

Источник