- С8С Станок токарно-винторезный универсальный (Болгария) паспорт, руководство, схемы, описание, характеристики
- Сведения о производителе токарно-винторезного станка С8С
- Станки, выпускаемые Болгарскими станкостроительными заводами
- С8С Станок токарно-винторезный универсальный. Назначение, область применения
- Основные технические характеристики токарно-винторезного станка С8С
- Шпиндель токарно-винторезного станка С8С
- Подачи и резьбы токарно-винторезного станка С8С
- Габариты рабочего пространства токарного станка С8С. Эскиз суппорта
- Общий вид токарно-винторезного станка С8С
- Расположение составных частей и органов управления токарным станком С8С
- Перечень составных частей органов управления токарного станка С8С
- Схема кинематическая токарно-винторезного станка С8С
- Краткое описание основных узлов станка С8С
- Шпиндель токарно-винторезного станка С8С
- Схема электрическая принципиальная токарно-винторезного станка С8С
- С8С Станок токарно-винторезный универсальный. Видеоролик.
- Определение общего числа ступеней скорости
- Построение структурных сеток и графиков частот вращения
С8С Станок токарно-винторезный универсальный (Болгария)
паспорт, руководство, схемы, описание, характеристики
Сведения о производителе токарно-винторезного станка С8С
Изготовитель токарно-винторезного станка С8С — предприятие Завод металлорежущих машин «Металлик», г. Пазарджик, ЗММ — Сливен АД Болгария.
Станки, выпускаемые Болгарскими станкостроительными заводами
С8С Станок токарно-винторезный универсальный. Назначение, область применения
Токарно-винторезный станок С8С предназначен для выполнения различных токарных работ и нарезания метрической, модульной, дюймовой и питчевой резьб. Обрабатываемые детали устанавливаются в центрах или патроне.
Универсальный токарный станок С8С оснащен 12 скоростными ступенями частоты вращения шпинделя.
Станок С8С можно настроить для нарезания метрической, дюймовой, модульной и питчевой резьбы, как это указано на лицевой табличке станка.
Шпиндельная система, зубчатые трансмиссии и другие механизмы в коробке скоростей смазываются автоматически через зубчатый масляный насос и путем разбрызгивания.
Основные технические характеристики токарно-винторезного станка С8С
Изготовитель — Завод металлорежущих машин «Металлик», г. Пазарджик, ЗММ — Сливен АД.
- Наибольший диаметр заготовки типа Диск, обрабатываемой над станиной — Ø 300 мм
- Наибольший диаметр заготовки типа Вал, обрабатываемой над суппортом — Ø 165 мм
- Расстояние между центрами — 762 мм
- Высота центров — 150 мм
- Мощность электродвигателя — 3,2 кВт
- Вес станка полный — 0,68 т
Шпиндель токарно-винторезного станка С8С
- Конец шпинделя — ИСО 702-3-75 ГОСТ 12593 (Концы шпинделей фланцевые под поворотную шайбу и фланцы зажимных устройств)
- Номинальный диаметр конуса D = 82,563 мм, условный размер конца шпинделя — 5
- Внутренний (инструментальный) конус шпинделя — Морзе 6
- Диаметр сквозного отверстия в шпинделе — Ø 32 мм
- Наибольший диаметр обрабатываемого прутка — Ø 30 мм
- Пределы чисел прямых оборотов шпинделя в минуту (12 ступеней) — 85..2000 об/мин
Подачи и резьбы токарно-винторезного станка С8С
- Пределы продольных подач — (48 ступеней) 0,006..1,77 мм/об
- Пределы поперечных подач — (48 ступеней) 0,008..0,885 мм/об
- Пределы шагов резьб метрических — (43 шага) 0,1..28 мм
- Пределы шагов резьб модульных — (19 шагов) модулей
- Пределы шагов резьб дюймовых — (53 шага)75..2,5 ниток на дюйм
- Пределы шагов резьб питчевых — (19 шагов) 70..4 питчей
Габариты рабочего пространства токарного станка С8С. Эскиз суппорта
Габариты рабочего пространства токарного станка c8c
Общий вид токарно-винторезного станка С8С
Фото токарного станка c8c
Фото токарного станка c8c
Фото коробки передач токарного станка c8c
Фото коробки подач токарного станка c8c
Расположение составных частей и органов управления токарным станком С8С
Расположение составных частей и органов управления токарным станком c8c
Перечень составных частей органов управления токарного станка С8С
- Крышка гитары
- Рукоятка переключения на «левую» и «правую» резьбу
- Рукоятка переключения двойного зубчатого блока
- Рукоятка переключения тройного зубчатого блока
- Рукоятка переключения двойного зубчатого блока
- Рукоятка переключения прямого или обратного хода или для включения вращения шпинделя
- Рукоятка ручного перемещения верхнего суппорта
- Рукоятка зажима пиноли
- Рукоятка зажима задней бабки
- Маховик перемещения пиноли
- Включатель охлаждающего устройства
- Главный выключатель
- Рукоятка для выбора шагов подачи или резьбы
- Рукоятка для выбора шагов подачи или резьбы
- Крышка инструментального шкафа
- Рукоятка для включения и выключения разъемной гайки ходового винта
- Рукоятка включения и выключения подачи суппорта
- Рычаг управления продольных и поперечных движений
- Маховик ручного продольного движения суппорта
- Рукоятка для переключения движения к ведущему валу или ведущему винту
Схема кинематическая токарно-винторезного станка С8С
Кинематическая схема токарного станка c8c
Краткое описание основных узлов станка С8С
Левая многодисковая фрикционная муфта на приемном валу коробки скоростей — для прямого вращения шпинделя, правая муфта для обратного вращения.
Шпиндель токарно-винторезного станка С8С
Шпиндель токарно-винторезного станка с8с
Схема электрическая принципиальная токарно-винторезного станка С8С
Электрическая схема токарного станка c8c
С8С Станок токарно-винторезный универсальный. Видеоролик.
Источник
Определение общего числа ступеней скорости
Для геометрического ряда частот вращения число ступеней скорости z, может быть определено из соотношения:

Вычисленная по этой формуле величина z округляется до целого числа, что приводит к некоторому изменению действительного диапазона регулирования Rn.
Выбор конструктивных вариантов привода
При настройке последовательно включенными групповыми передачами число ступеней скорости z может быть представлено в виде:
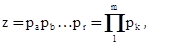
где pk – число отдельных передач в каждой группе;
m – число групп передач.
При выбранном числе ступеней частот вращения шпинделя z количество групп передач, количество передач в каждой группе и порядок расположения групп может быть различным.
Число конструктивных вариантов привода Nкон состоящего из m групп передач, определяется по формуле:

где q – число групп с одинаковым числом передач.
Определение числа возможных кинематических вариантов
Если частоты вращения шпинделя изменяются по геометрическому ряду, то передаточные отношения передач в группах образуют геометрический ряд со знаменателем j х , где х – целое число, называемое характеристикой группы передач. Для последовательного получения частот вращения шпинделя сначала переключают передачи одной группы, затем другой и т.д.
В зависимости от принятого порядка переключений группа может быть:
а) основной, характеристика, которой определяется по формуле:
б) первой переборной группой, для которой характеристика определяется по формуле:
где р1 – число передач в основной группе.
в) второй переборной группой, для которой характеристика определяется по формуле:
где р2 – число передач в первой переборной группе.
Основной и различными по номеру переборными группами может быть любая группа передач в приводе. Для определенного конструктивного варианта число кинематических Nкин будет равно числу перестановок из m групп передач:
Nкин. = m!, (3.8)
Определение максимальных передаточных отношений по группам передач
Общее максимальное передаточное отношение привода umax, определяется по формуле:
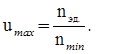
Поученное передаточное отношение может быть представлено в виде:
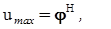
где Н – показатель степени, определяющий величину общего передаточного отношения.
Определение максимальных передаточных отношений в группах производится путем разбиения общего передаточного отношения на передаточные отношения групп, для чего вычисляется показатель степени Н и выражается в виде:

где hk – показатель степени, характеризующий величину максимального передаточного отношения k-той группы передач;
m – число групп передач.
При этом выбранные значения hk должны быть целыми числами и должны удовлетворять условию:
Максимальное передаточное отношение в группе umaxk, определится по формуле:

При этом должно быть обеспечено выполнение следующего условия:

Так как показатель степени Н, как правило, не является целым числом, он не может быть точно представлен суммой целых чисел. Поэтому для сохранения величины общего максимального передаточного отношения вводится дополнительная передача от вала электродвигателя на входной вал, передаточное отношение которой, определится по формуле:

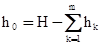
Источник
Построение структурных сеток и графиков частот вращения
ЗАДАНИЕ № 4
Построение структурных сеток и графиков частот вращения
Расчет числа зубьев передач
Теоретическая часть
Для обеспечения необходимой точности настройки станка на заданную скорость резания необходимо иметь возможность устанавливать различную частоту вращения шпинделя в пределах от nmin до nmax, рассчитываемые по уравнению:
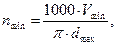 |
где V – скорость резания, м/мин;
d – диаметр заготовки или инструмента, мм.
Диапазон регулирования частоты вращения шпинделя определяется по формуле:
и характеризует эксплутационные возможности станка.
Большое количество находящихся в эксплуатации станков имеют ступенчатые ряды частот вращения. Поэтому вместо частоты, обеспечивающей рассчитанную оптимальную скорость резания при заданном диаметре, приходится выбрать ближайшую меньшую из имеющихся на станке. Этой действительной частоте nД будет соответствовать действительная скорость резания
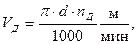 |
которая меньше расчетной на V − VД.
Относительную потерю скорости резания определяют уравнением:
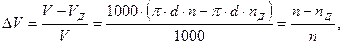 |
которая будет тем меньше, чем меньше разность: n − nД. Наиболее рационально частоты вращения от n minдо nmaxрасполагать в геометрической прогрессии со знаменателем φ, т.е. соблюдать соотношение:
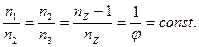 |
Значение знаменателя геометрической прогрессии выбирается по приложению (табл. А1).
Совокупность передач, связывающих вращение двух соседних валов, образует группу передач. Ее характеризуют два показателя:
• количество передачв группе р;
• величины их передаточных отношений i.
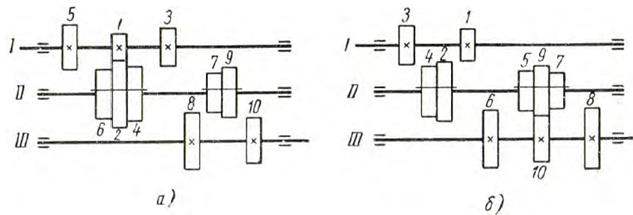
Рассмотрим для простоты устройство шести ступенчатой коробки скоростей (рис. 1, а).
Для передачи вращения от вала I валу II служит множительный механизм с трехвенцовым блоком(колеса 1-2, 3-4, 5-6).
Для передачи вращения от вала II валу III – множительный механизм с двухвенцовым блоком(колеса 7-8, 9-10).
В результате последовательного соединения этих механизмов (обычная множительная структура) при одной скорости ведущего вала I ведомый вал III (или шпиндель) может иметь шесть различных угловых скоростей.
В рассматриваемой схеме мы имеем две множительные группы:
• первая состоит из трех передач (1-2; 3-4, 5-6);
• вторая – из двух передач (7-8, 9-10).
Порядок чередования групп вдоль кинематической цепи характеризует конструктивный вариант коробки.
Его условно можно выразить в виде структурной формулы:
z = 6 = 3 . 2.
Рис. 1 – Схема шести ступенчатой коробки скоростей
Другой конструктивный вариант (порядок) имеет схема шести ступенчатой коробки скоростей (рис. 1, б). Здесь:
• в первой группе две передачи (1-2, 3-4);
• во второй – три передачи (5-6, 7-8, 9-10).
Структурная формула для этого варианта:
Количество возможных конструктивных вариантов одной и той же структуры равно числу перестановок m групп:
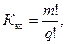 |
q – число групп с одинаковым количеством передач.
Для нашего случая: число перестановок m = 2,число групп q = 1, следовательно Ккс = (1 . 2 )/ 1 = 2, а именно:
z = 6 = 3 . 2 = 2 . 3.
Отношение передаточных отношений передач в группе изменяется в φ x раз и обусловлено кинематическим порядком (или вариантом) включения передач при переходе от одной скорости вращения шпинделя к другой.
Показатель степени хназывается характеристикой группы. Структурную формулу, уточняющую не только конструктивный, но и кинематический порядок, принято записывать так:
Здесь место группы в формуле показывает конструктивный порядок и номер группы, а индекс – ее характеристику.
Для нашего примера z = 6 = 31 . 23.
Такая запись означает:
• первая группа имеет три передачи, а ее характеристика x1= 1;
• вторая группа – две передачи, а характеристика x2= 3 .
Группу передач, имеющую характеристику х = 1, называютосновной группой,остальные группы (при х > 1)– переборными.
Величина х в общем случае не может быть произвольной.
Если первая группа является основной, то характеристика последующих групп равна числу ступеней скорости полученных совокупностью групповых передач, кинематически предшествующих данной группе. Это положение на основании уравнения (1) представляется в следующем виде.
Например:
Z = 8 = 21 . 22 . 24;
Z = 12 = 31 . 23 . 26;
Z = 18 = 31 . 33 . 29.
Возможны и другие кинематические варианты.
Общее их количество равно числу перестановок из m элементов, т. е. Ккинем. = m!.
Для нашего примера Ккинем. = 1 . 2 = 2.
Общее количество К возможных вариантов (конструктивных и кинематических) для обычных множительных структур равно:
Пример построения структурной сетки
В качестве примера возьмем привод (рис. 2), обеспечивающий двенадцать ступеней скорости (частот вращения) за счет последовательного соединения трех двухваловых шестеренных коробок (групп передач): одной на три ступени (передачи) и двух на две.
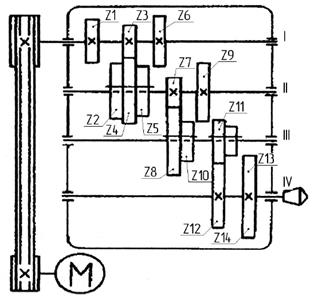 |
Рис. 2 – Кинематическая схема привода на 12 ступеней скоростей
Его структурная формула будет иметь вид Z = 3 . 2 . 2 = 12. Если в структурной формуле цифрами в скобках обозначить характеристики групп, например,
то получим один из вариантов структурной формулы.
Перваяв конструктивном отношении группа передач является основной (ее характеристика X0= 1 ), т.е. она состоит из передач, отношение соседних по значению передаточных отношений которых равно φ 1 .
Вторая группа передач является первой переборной с характеристикой, равной числу передач в основной группе, т.е. X2= 3, а отношение соседних по значению передаточных отношений в ней равно φ 3 .
Третья группа передач – вторая переборная. Ее характеристика равна произведению числа передач в основной и первой переборной группах, т.е. X3= 3 . 2 = 6, а отношение соседних по значению передаточных отношений в ней равно φ 6 .
Принципиально возможны варианты структурных формул, а значит, и конструкций приводов, полученные путем изменения конструктивного (последовательности расположения групп) и кинематического (изменения значения характеристик) порядка, например:
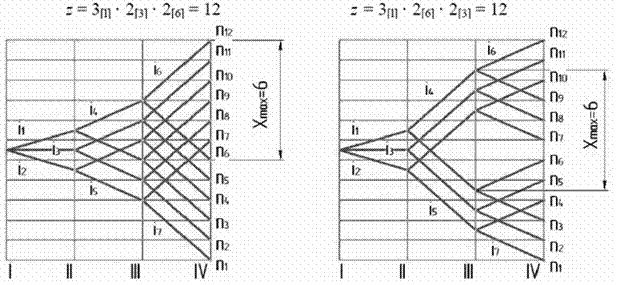 |
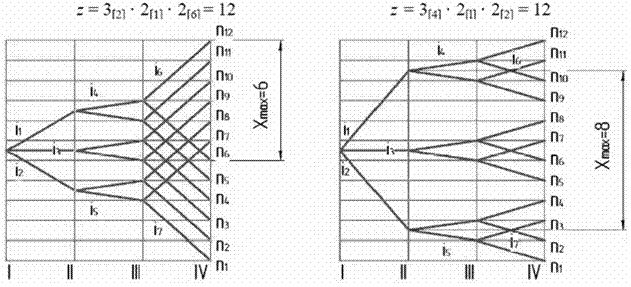 |
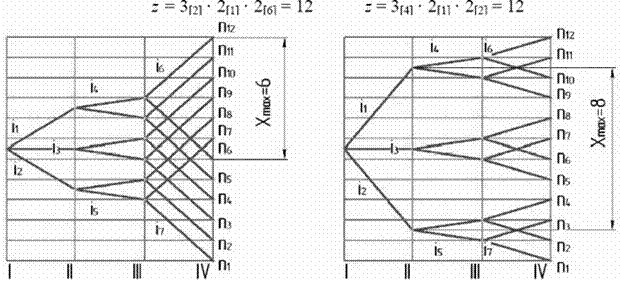 |
Рис. 3 – Варианты структурных сеток для Z = 3 . 2 . 2 = 12
Для принятого конструктивного варианта (рис. 3) можно написать шесть вариантов структурных формул:
и построить шесть вариантов структурных сеток (рис. 3).
После построения всех вариантов структурных сеток выбирают оптимальный вариант.
При выборе оптимального варианта структурной сетки (варианта структурной формулы) необходимо учитывать следующее.
1) Во избежание чрезмерно больших диаметров зубчатых колес в коробках скоростей, а также в целях нормальной их работы практикой рекомендованы следующие предельные передаточные отношения в группах:
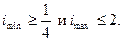 |
Следовательно, наибольший диапазон регулирования в группе равен:
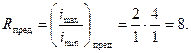 |
Поэтому необходимо сначала определить диапазон регулирования в последней переборной группе для всех структурных сеток (при выбранном значении φ) и исключить из дальнейшего рассмотрения варианты, не удовлетворяющие условию:
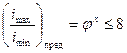 |
В нашем примере:
для вариантов 1), 2), 3), 5) Xmax= 6;
Если знаменатель ряда φ частот вращения шпинделя выбран равным 1,26, то согласно табл. 1, для φ = 1,26, Xmax = 9 следовательно, все варианты структурных сеток удовлетворяют указанному условию.
Если выбран φ = 1,41, то из рассмотрения следует исключить варианты 4) и 6).
При φ = 1,58и более ни один из вариантов непригоден.
Таблица 1 – Максимально допустимые величины Хmax
| Для коробок | φ | |||||
| 1,06 | 1,12 | 1,26 | 1,41 | 1,58 | 1,78 | 2,0 |
| скоростей | ||||||
| подач |
2) Далее выбирают структурные сетки, у которых:
− в качестве основной и первой в конструктивном порядке взята группа с наибольшим числом ступеней;
− переборные расположены в порядке убывания числа их ступеней.
3) Из всех вариантов, удовлетворяющих данному условию, выбирают:
− вариант с наиболее плотным расположением лучей в первых в конструктивном порядке передачах.
С учетом перечисленных рекомендаций обычно наиболее оптимальным, и для рассматриваемого примера в том числе, вариантом структурной сетки будет (рис. 4):
Здесь лучи располагаются более тесно.
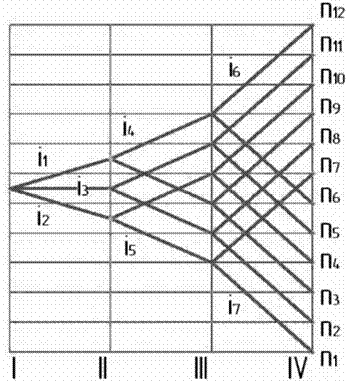 |
Рис. 4 – Структурная сетка привода: z = 3(1) . 2(3) . 2(6) = 12.
Выбрав оптимальный вариант структурной сетки, приступают к построению графика частот вращения.
Алгоритм построения графика частот вращения (чисел оборотов)
Для построения графика частот вращения должны быть известны:
а) φ – знаменатель ряда частот вращения;
в) n0– число оборотов выбранного приводного электродвигателя;
г) полная кинематическая схема привода.
График частот вращения строится на поле, аналогичном полю для построения структурных сеток, увеличив число вертикальных линий на одну (на вал приводного двигателя), и вместо порядковых номеров частот горизонтальным линиям присваивают их фактические значения.
Сначала на этом поле, соединяя лучами линии валов, намечают цепь передач для снижения чисел оборотов с n0 до n1. Для этого используют одну передачу каждой группы, в том числе и ременную, соединяющую вал двигателя и входной (первый) вал коробки, если она предусмотрена в кинематической схеме.
Передаточные отношения этих передач распределяют таким образом, чтобы редукция от входной передачи к выходной плавно нарастала. При этом подразумевается, что:
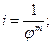
− если луч отклоняется вниз, то передача понижающая, т.е.
− если вверх – повышающая, т.е. i = φ m ;
− для горизонтального луча i = φ 0 = 1.
При построении графика чисел оборотов необходимо выбирать на промежуточных валах такие точки, чтобы передаточные отношения были в пределах допустимых:
Для ременных передач передаточные отношения рекомендуется выбирать в пределах:
− знаменатель ряда φ =1,26;
− минимальное число оборотов шпинделя n1= 50 об / мин;
− число оборотов приводного электродвигателя nэ= 1440 об / мин.
Задание
1 Составить кинематическую схему трех валовой коробки скоростей.
2 Рассчитать геометрический ряд частот вращения на выходном валу.
По приложению Б (таблица Б.1) выбирать ближайшие стандартные значения частот вращения.
3 Построить структурные сетки для кинематических вариантов.
4 Построить график частот вращения.
5 Рассчитать значения передаточных отношений.
6 Определить числа зубьев передач.
7 Выполнить проверку. Определить nminпо рассчитанной коробке скоростей.
Исходные данные
− число скоростей шпинделя z = 9;
− структурная формула z = 3 . 3 = 9;
− знаменатель ряда частот вращения φ =1,26;
− минимальное число оборотов шпинделя nmin = 160 об/мин;
− частота вращении ведущего вала n = 1000 об/мин.
ЗАДАНИЕ № 4
Построение структурных сеток и графиков частот вращения
Расчет числа зубьев передач
Теоретическая часть
Для обеспечения необходимой точности настройки станка на заданную скорость резания необходимо иметь возможность устанавливать различную частоту вращения шпинделя в пределах от nmin до nmax, рассчитываемые по уравнению:
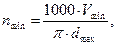 |
где V – скорость резания, м/мин;
d – диаметр заготовки или инструмента, мм.
Диапазон регулирования частоты вращения шпинделя определяется по формуле:
и характеризует эксплутационные возможности станка.
Большое количество находящихся в эксплуатации станков имеют ступенчатые ряды частот вращения. Поэтому вместо частоты, обеспечивающей рассчитанную оптимальную скорость резания при заданном диаметре, приходится выбрать ближайшую меньшую из имеющихся на станке. Этой действительной частоте nД будет соответствовать действительная скорость резания
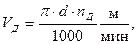 |
которая меньше расчетной на V − VД.
Относительную потерю скорости резания определяют уравнением:
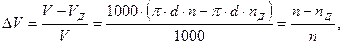 |
которая будет тем меньше, чем меньше разность: n − nД. Наиболее рационально частоты вращения от n minдо nmaxрасполагать в геометрической прогрессии со знаменателем φ, т.е. соблюдать соотношение:
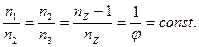 |
Значение знаменателя геометрической прогрессии выбирается по приложению (табл. А1).
Совокупность передач, связывающих вращение двух соседних валов, образует группу передач. Ее характеризуют два показателя:
• количество передачв группе р;
• величины их передаточных отношений i.
Рассмотрим для простоты устройство шести ступенчатой коробки скоростей (рис. 1, а).
Для передачи вращения от вала I валу II служит множительный механизм с трехвенцовым блоком(колеса 1-2, 3-4, 5-6).
Для передачи вращения от вала II валу III – множительный механизм с двухвенцовым блоком(колеса 7-8, 9-10).
В результате последовательного соединения этих механизмов (обычная множительная структура) при одной скорости ведущего вала I ведомый вал III (или шпиндель) может иметь шесть различных угловых скоростей.
В рассматриваемой схеме мы имеем две множительные группы:
• первая состоит из трех передач (1-2; 3-4, 5-6);
• вторая – из двух передач (7-8, 9-10).
Порядок чередования групп вдоль кинематической цепи характеризует конструктивный вариант коробки.
Его условно можно выразить в виде структурной формулы:
z = 6 = 3 . 2.
Рис. 1 – Схема шести ступенчатой коробки скоростей
Другой конструктивный вариант (порядок) имеет схема шести ступенчатой коробки скоростей (рис. 1, б). Здесь:
• в первой группе две передачи (1-2, 3-4);
• во второй – три передачи (5-6, 7-8, 9-10).
Структурная формула для этого варианта:
Количество возможных конструктивных вариантов одной и той же структуры равно числу перестановок m групп:
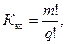 |
q – число групп с одинаковым количеством передач.
Для нашего случая: число перестановок m = 2,число групп q = 1, следовательно Ккс = (1 . 2 )/ 1 = 2, а именно:
z = 6 = 3 . 2 = 2 . 3.
Отношение передаточных отношений передач в группе изменяется в φ x раз и обусловлено кинематическим порядком (или вариантом) включения передач при переходе от одной скорости вращения шпинделя к другой.
Показатель степени хназывается характеристикой группы. Структурную формулу, уточняющую не только конструктивный, но и кинематический порядок, принято записывать так:
Здесь место группы в формуле показывает конструктивный порядок и номер группы, а индекс – ее характеристику.
Для нашего примера z = 6 = 31 . 23.
Такая запись означает:
• первая группа имеет три передачи, а ее характеристика x1= 1;
• вторая группа – две передачи, а характеристика x2= 3 .
Группу передач, имеющую характеристику х = 1, называютосновной группой,остальные группы (при х > 1)– переборными.
Величина х в общем случае не может быть произвольной.
Если первая группа является основной, то характеристика последующих групп равна числу ступеней скорости полученных совокупностью групповых передач, кинематически предшествующих данной группе. Это положение на основании уравнения (1) представляется в следующем виде.
Например:
Z = 8 = 21 . 22 . 24;
Z = 12 = 31 . 23 . 26;
Z = 18 = 31 . 33 . 29.
Возможны и другие кинематические варианты.
Общее их количество равно числу перестановок из m элементов, т. е. Ккинем. = m!.
Для нашего примера Ккинем. = 1 . 2 = 2.
Общее количество К возможных вариантов (конструктивных и кинематических) для обычных множительных структур равно:
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Источник