Арифметическое действие второй ступени

Порядок выполнения действий, правила, примеры.

Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Выполните действия 7−3+6 .

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .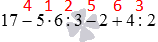

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.

Рассмотрим решения примеров.

Выполните действия в выражении (3+1)·2+6 2 :3−7 .

В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .

Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .

Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.

Источник

Действия первой и второй ступени

Арифметические действия делятся на действия первой и второй ступени.

Действия первой ступени — это сложение и вычитание:

7 — 3 — вычитание.

Действия второй ступени — это умножение и деление:

5 · 4 — умножение,

Порядок действий

Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.

Пример 1. Вычислить значение выражения:

15 + 17 — 20 + 8 — 12.

Решение: Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.

1	2	3	4
15	+	17	—	20	+	8	—	12

Пример 2. Вычислить значение выражения:

60 : 15 · 7 : 2 · 3.

Решение: Данное выражение содержит действия только одной ступени — второй (умножение и деление). Надо определить порядок действий и выполнить их.

1	2	3	4
60	:	15	·	7	:	2	·	3

Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.

Пример. Вычислить значение выражения:

24 : 3 + 5 · 2 — 17.

Решение: Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.

Источник

Урок математики «Действия первой и второй ступеней»

Тип урока: объяснение нового материала.

Цели урока:

• Формирование умения выполнять вычисления в выражениях без скобок.
• Развитие внимания и коммуникативных навыков (работа в парах).
• Воспитание культуры общения.

Оборудование: учебник, тетрадь для самостоятельных работ, рабочие тетради, сигнальные карточки.

I. Организационный момент

Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.

II. Актуализация знаний

Задание по вариантам.

Соедините линией карточку, на которой записано выражение, с карточкой, на которой записано его значение.

(У доски работают по 1 учащемуся от варианта, остальные самостоятельно, затем коллективная проверка).

– Что вам необходимо знать хорошо, чтобы без ошибок выполнить это задание? (таблицу умножения)
– С действиями деления и умножения мы познакомились в каком классе? (во втором)
– Какие действия над числами мы изучали в первом классе? (сложение и вычитание)

III. Изучение нового материала

– Сегодня на уроке будем работать с выражениями, в которых встречается эти действия.

1. Работа по учебнику с. 105, № 1

Вычисли устно значение следующих выражений.

25 + 15 – 10 = 30 25 – 10 + 15 = 30

Сложение и вычитание – это действия I ступени.

– В каком порядке в выражении без скобок выполняются действия I ступени? (По порядку слева направо)

2. Работа по учебнику с. 105, № 2

Вычисли устно значение следующих выражений:

Умножение и деление – это действия II ступени.

– В каком порядке в выражении без скобок выполняются действия II ступени? (По порядку слева направо)

Вывод:

Если в выражении без скобок присутствуют только действия одной ступени, то они выполняются по порядку слева направо.

3. Создание проблемной ситуации

Вычисли значение следующих выражений.

80 – 6 4 = 56 35 + 7 5 = 70

– С выполнения какого действия начинается вычисление значений данных выражений? (с умножения)

4. Знакомство с новым правилом.

Работа по учебнику С. 106.

Если в выражении без скобок присутствуют действия I и II ступеней, то сначала выполняются по порядку действия II ступени, а уже потом действия I ступени.

(Плакат с правилом учитель вывешивает на доску)

IV. Первичное закрепление

1. Работа по учебнику с. 106, №4

Вычисли значение следующих выражений, соблюдая порядок выполнения действий I и II ступеней (решение с комментированием)

55 – 10 : 2 + 50 = 100

258 + 15 : 5 – 8 9 = 189

2. Составление и решение задачи с. 106 №5

Задание. Составь задачу, решением которой было бы выражение 50 – 3 5. Вычисли и запиши ответ этой задачи.

Пример задачи, составленной учащимися.

В магазине было 50 кг бананов. За день продали 5 ящиков по 3 кг в каждом. Сколько кг бананов осталось?

Составление краткой записи задачи (1ученик у доски).

Было – 50 кг
Продали – 5 ящ. по 3кг
Осталось – ? кг

Ответ: осталось 25 кг бананов.

V. Физминутка

Раз, два, три, четыре, пять –
Все умеем мы считать,
Отдыхать умеем тоже.
Руки за спину заложим,
Голову поднимем выше
И легко – легко подышим.

VI. Самостоятельная работа (в парах ) с проверкой по образцу

1. Учитель: Работу выполняете в тетрадях для самостоятельных работ С.52, № 1

1 ряд – 1-2 пример,
2 ряд – 3-4 пример,
3 ряд – 5-6 пример.

У каждой пары на парте есть две сигнальные карточки. Одна красного цвета, а другая – зелёного цвета.
Если учащиеся в паре выполнили работу, на край стола выкладывают зелёную карточку.
Если есть затруднения, на край стола выкладывают красную карточку.
Выполнить правильно это задание вам поможет правило, с которым мы сегодня познакомились, оно на доске.

Проверьте правильность выполнения задания по образцу на доске.

32 + 6 7 – 14 = 60

300 – 2 8 + 27 : 9 = 287

20 + 9 2 – 28 = 10

205 + 8 7 – 63 : 9 = 254

1) 56,
2) 7,
3) 261,
4) 254 3 ряд

66 – 4 9 + 18 = 48

400 – 42 : 7 + 6 8 = 442

1) 6,
2) 48,
3) 394,
4) 442

– Пара учащихся, которая выполнила работу правильно ставит себе «+», а если допустили ошибку, то «–».
– При вычислении, какого действия допустили ошибку? (1 ряд – при умножении или делении чисел)
– Как вы думаете, почему была допущена ошибка? (Плохо знаем таблицу умножения)
– Что нужно сделать, чтобы в дальнейшем не допускать таких ошибок? (Хорошо выучить таблицу умножения)
– Кто допустил другую ошибку? (2 ряд – во втором примере другой ответ)
– Как вы думаете, почему так получилось? (Неправильно расставили порядок действий в выражении)
– Какое правило надо знать, чтобы правильно решать сложные выражения без скобок? (Учащийся повторяет изученное на уроке правило)

VII. Итог урока

– Что для себя нового вы сегодня узнали?

VII. Домашнее задание: с. 106, № 3, № 6.

Источник